笔记由本人根据材料整理，可能存在问题。

视频地址：https://www.bilibili.com/video/BV1W34y1i7xK

Github仓库地址：https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes

说明：本文档绝大部分图片来自于在线文档，侵权请联系我删除

一、前置概念介绍

1.1 欢迎

有关机器学习的案例：

其中包括培养计算机的新能力，事实上机器学习已经成为计算机的一个能力。将机器学习运用到数据挖掘、一些人类无法编程的工作、自我服务的项目和理解人类的学习和了解大脑。

1.2 机器学习是什么？

实际上并没有一个被广泛认可的定义。

第一个机器学习的定义是：在进行特定编程的情况下，给予计算机学习能力的领域。(不太正式)

另一个年代近一点的定义：一个程序被认为能从经验E中学习，解决任务T，达到性能度量值P，当且仅当，有了经验E后，经过P评判，程序在处理T时的性能有所提升。

以垃圾邮件分类问题为例子：

• T为对收到的邮件进行分类（依照是否是垃圾邮件）

• E为例次进行分类积累得到的经验（例如一些垃圾邮件存在的共同特征）

• P为分类成功的比例

可简称为 Task Experience Performance

目前存在的最主要的两种学习算法：

• 监督学习：教计算机如何去完成任务

• 无监督学习：让计算机自己进行学习

1.3 监督学习

监督学习是有正确答案的预测，分为：

• 回归问题 连续值 房价预测问题

• 分类问题 离散值 肿瘤分类问题

给出例子：

房价预测

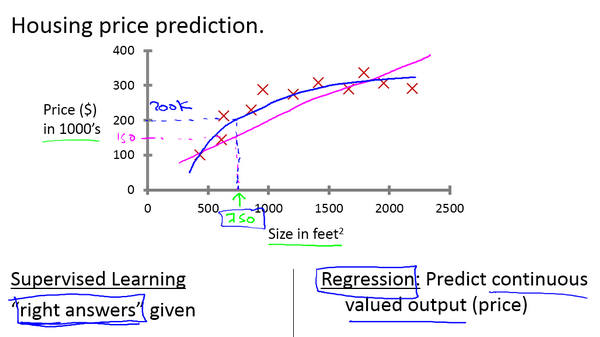
在这个例子中，我们需要找到一条曲线（直线）能够尽量多得穿过给出的数据点（当然也不是要全部穿过，这会出现过拟合现象），决定用直线还是二次方程来拟合数据，这便是监督学习算法需要完成的工作。

房价预测问题属于回归问题，推测结果属于连续值

回归的意思是指我们试着推测出这一系列连续值属性

肿瘤分类

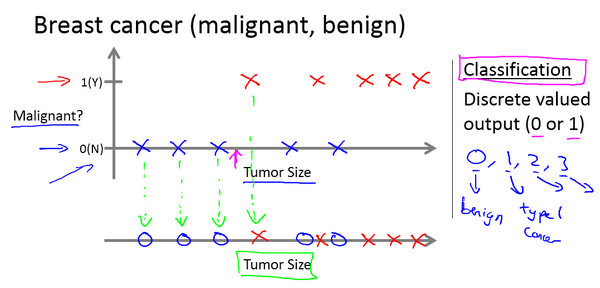
在这个例子中，我们试着推测出离散的输出值：0或1良性或恶性。

肿瘤分类问题属于分类问题，但事实上在分类问题中输出可能不止两个值。

分类问题的输出通常是是离散值。

监督学习的基本思想是：我们数据集中的每个样本都有相应的“正确答案”。再根据这些样本作出预测。

我的补充理解：在监督学习中正确的答案是给出的，也就是输入会有对应的正确结果，我们要做的就有训练一个模型，该模型能够使我们输入的测试数据能够获取正确的输出结果，在此基础上我们能够通过该模型对尚未知道结果的输入数据进行相对准确的结果预测。

1.4 无监督学习

无监督学习是对未知数据提取特征的算法

• 聚类 客户特征群体划分问题

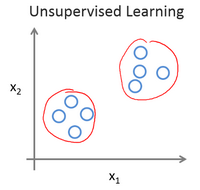
无监督学习中没有任何的标签或者是有相同的标签或者就是没标签，在一个给出的数据集中，我们对于其中的数据没有任何的认识。而无监督学习算法做的就是找出数据集的特征并将数据划入不通过的聚类簇，所以也叫做聚类算法。

DNA微观数据例子：

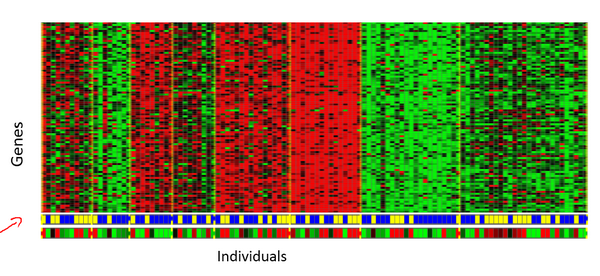
基本思想是输入一组不同个体，对其中的每个个体，你要分析出它们是否有一个特定的基因。我们要做的是运行一个聚类算法，把个体聚类到不同的类或不同类型的组（人）

应用场景：

• 组织大型计算机集群，提高数据中心工作效率

• 社交网络的分析

• 消费者市场分割

• 天文数据分析

注意：聚类只是无监督学习算法的一种

典型示例：鸡尾酒宴问题、新闻事件分类、细分市场

第二部分开始介绍特定的学习算法，包括其工作原理和实现方法

二、单变量线性回归

2.1 模型表示

第一个学习算法是线性回归算法。

给出例子：

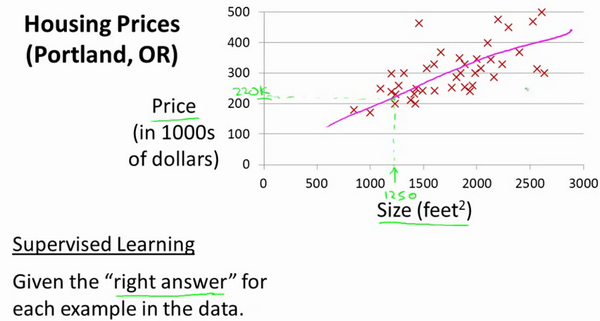
本例是监督学习，可以看到正确的答案（输出）已经给出，房屋大小与价格相对应。本例需要预测的输出值（房价）是连续值，属于监督学习中的回归问题。

在整个课程中小写m用于表示训练样本的数量，训练样本来源于训练集

以上图为例给出相应的训练集，如下图所示：

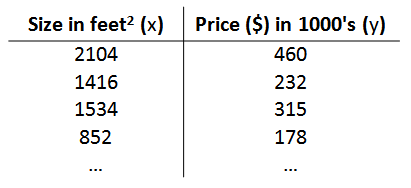
对其中的数据进行标记：

m代表训练集中实例的数量

x代表特征/输入变量

y代表目标变量/输出变量

(x，y)代表训练集中的实例

(x⁽ⁱ⁾,y⁽ⁱ⁾)代表第 i 个观察实例

h代表学习算法的解决方案或函数也称为假设（hypothesis）

监督学习算法工作流程如下图所示：

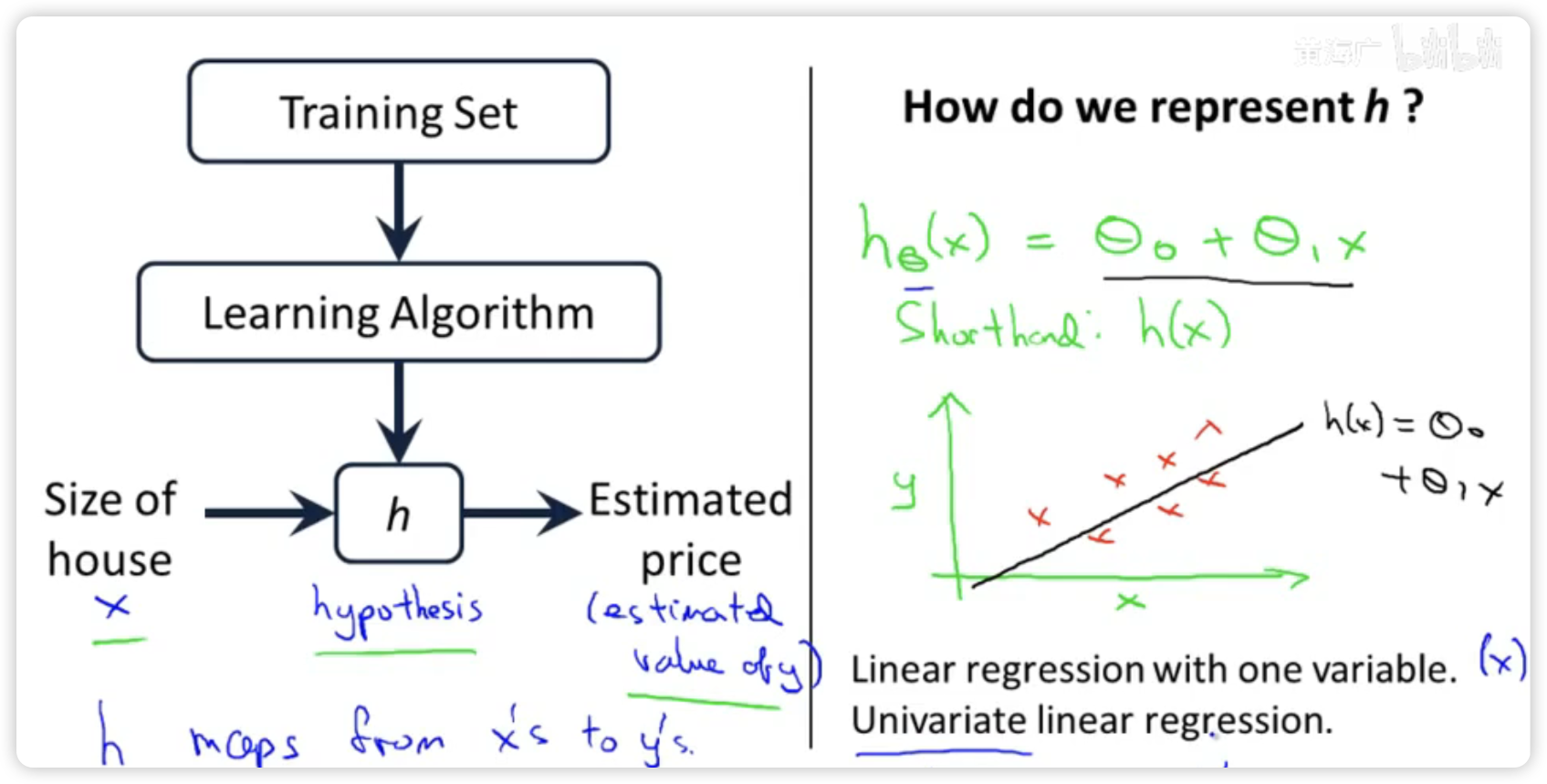
1. 将训练集喂给学习算法工作，使其输出一个函数h，h代表hypothesis(假设)。

2. 输入x，在这里是房子的大小

3. 函数h(x)经过运算输出y，在这里是房子的预测价格

Q：如何表示假设的h函数?

A：一种可能的表达方式为h(x) = theta0 + theta1 * x，只有一个特诊/输入变量，故这样的问题叫做单变量线性回归问题。

2.2 代价函数

如何选择参数theta使得假设函数h预测的结果y与实际给出的训练集中的y误差最小

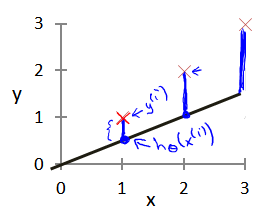
给出平方差和定义的代价函数

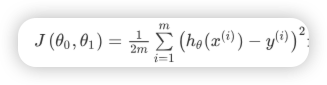
2.3 代价函数的直观理解I

探究假设函数h(x)和损失函数J(theta)之间的关系

通过计算损失函数J（cost function）最小值，找到符合条件的假设函数h(x)中的参数，使得假设函数能够很好地拟合到给出的数据集，以此来确保通过假设函数h（x）能够对输入的数据预测到相对精确的结果。

拟合越好，损失越小，但也要防止过度拟合，过度拟合会使假设函数h(x)对新样本的表现不好。

2.4 代价函数的直观理解II

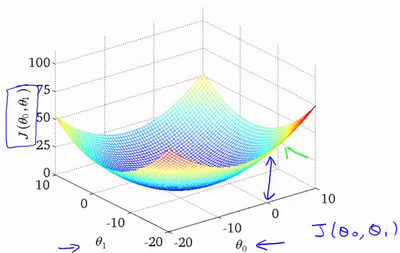
上图为等高线图，横轴为参数theta0和theta1，纵轴为损失函数J(theta0,theta1)，可以看到在三维空间中存在一个使得J(theta0,theta1)最小的点，该位置便是我们需要寻找的全局最优解，当theta处于这个位置时，损失函数达到最小，假设函数与数据集的拟合程度最高，假设函数的预测准确率也达到最高。

2.5 梯度下降

梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数J(theta0,theta1)的最小值。

使用梯度下降算法将代价函数最小化

具体实现流程如下图所示：

注意在梯度下降时参数theta是同时更新的，先后不同步更新会使梯度下降算法产生问题，无法找到最适合最小化代价函数J的参数theta。

2.6 梯度下降的直观理解

梯度下降算法如下：

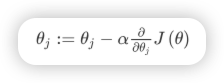
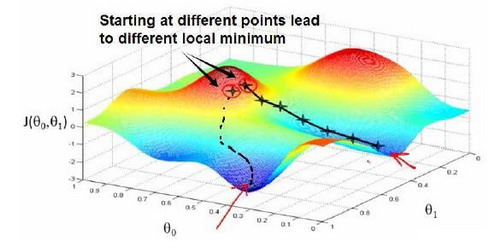
具体解释：

对参数theta赋值，使得按梯度下降最快方向进行，一直迭代下去，最终得到局部最小值。其中 阿尔法 是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。

设置不同学习速率存在的两种情况

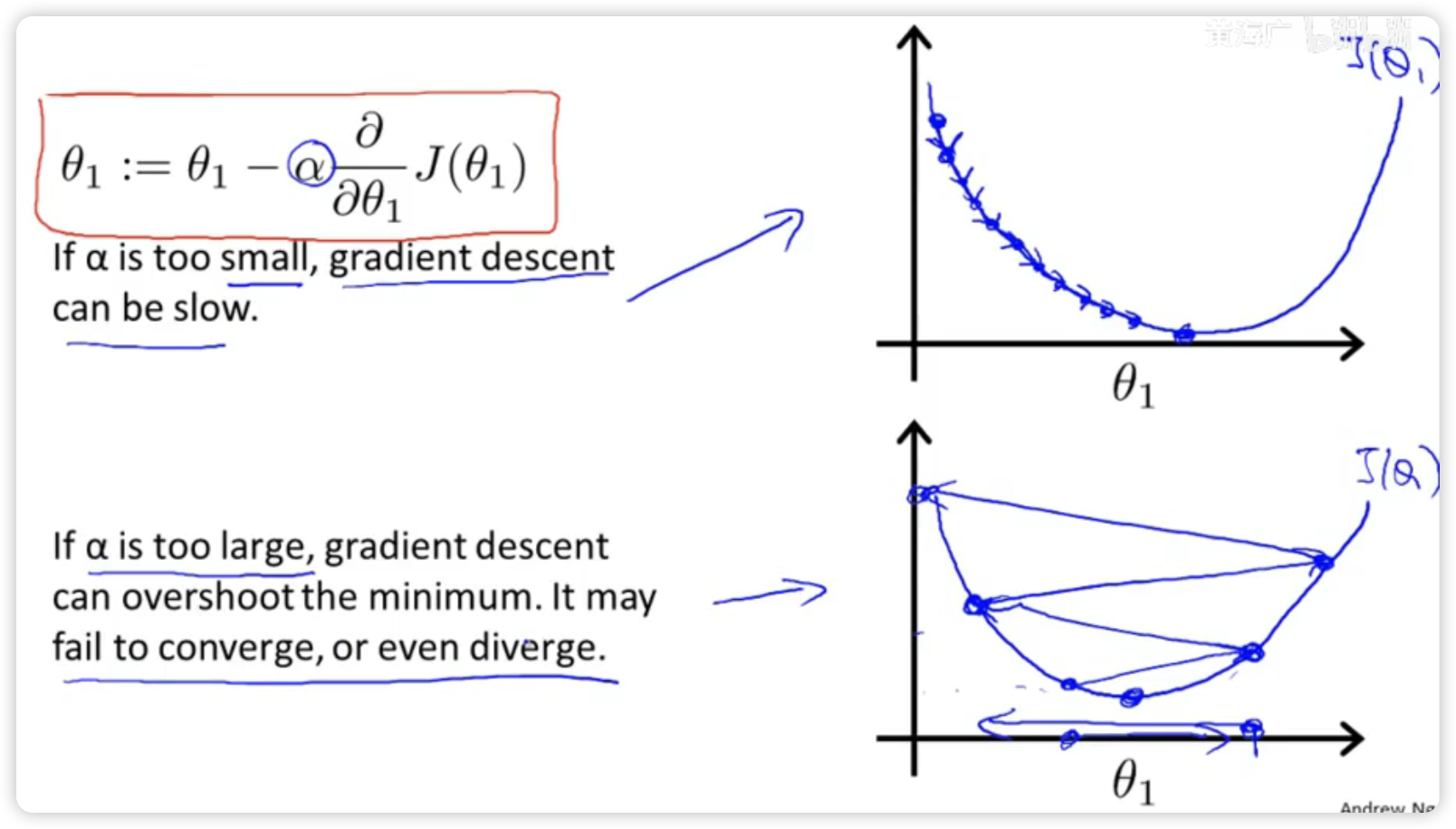
• 如果a太小的话，可能会很慢，因为它会一点点挪动，它会需要很多步才能到达全局最低点

• 如果a太大，它会导致无法收敛，甚至发散。

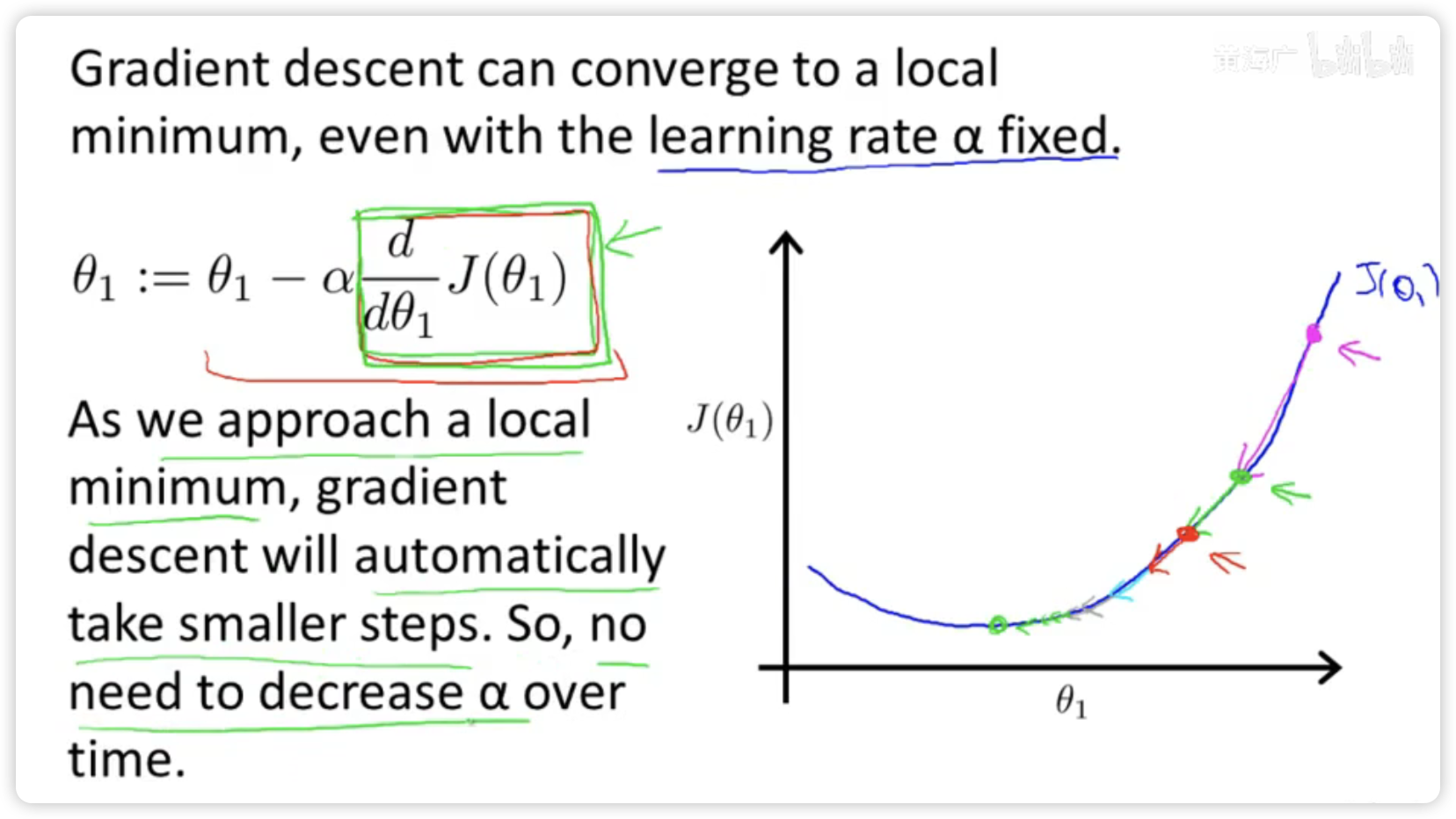
即使学习速率a保持不变时，梯度下降也可以收敛到局部最低点。

你可以用梯度下降算法来最小化任何代价函数，不只是线性回归中的代价函数。

2.7 梯度下降的线性回归

梯度下降是很常用的算法，它不仅被用在线性回归上和线性回归模型、平方误差代价函数，也可以与代价函数结合。

梯度下降算法和线性回归算法比较如下图所示：

对我们之前的线性回归问题运用梯度下降法，算法改写为：

2.8 接下来的内容

对线性代数进行一个快速的复习回顾，通过它们，你可以实现和使用更强大的线性回归模型。

三、线性代数回顾(Linear Algebra Review)

推荐观看麻省理工学院 - MIT - 线性代数和线性代数的本质

四、多变量线性回归(Linear Regression with Multiple Variables)

4.1 多维特征

4.2 多变量梯度下降

4.3 梯度下降法实践1-特征缩放

4.4 梯度下降法实践2-学习率

4.5 特征和多项式回归

4.6 正规方程

4.7 正规方程及不可逆性（选修）

五、Octave教程(Octave Tutorial)

本人采用Python语言进行本课程的学习，此部分不做笔记记录。

六、逻辑回归(Logistic Regression)

6.1 分类问题

6.2 假说表示

6.3 判定边界

6.4 代价函数

6.5 简化的成本函数和梯度下降

6.6 高级优化

6.7 多类别分类：一对多

七、正则化(Regularization)

7.1 过拟合的问题

7.2 代价函数

7.3 正则化线性回归

7.4 正则化的逻辑回归模型

第八、神经网络：表述(Neural Networks: Representation)

8.1 非线性假设

8.2 神经元和大脑

8.3 模型表示1

8.4 模型表示2

8.5 样本和直观理解I

8.6 样本和直观理解II

8.7 多类分类

九、神经网络的学习(Neural Networks: Learning)

9.1 代价函数

9.2 反向传播算法

9.3 反向传播算法的直观理解

9.4 实现注意：展开参数

9.5 梯度检验

9.6 随机初始化

9.7 综合起来

9.8 自主驾驶

十、应用机器学习的建议(Advice for Applying Machine Learning)

10.1 决定下一步做什么

10.2 评估一个假设

10.3 模型选择和交叉验证集

10.4 诊断偏差和方差

10.5 正则化和偏差/方差

10.6 学习曲线

10.7 决定下一步做什么

十一、机器学习系统的设计(Machine Learning System Design)

11.1 首先要做什么

11.2 误差分析

11.3 类偏斜的误差度量

11.4 查准率和查全率之间的权衡

11.5 机器学习的数据

十二、支持向量机(Support Vector Machines)

12.1 优化目标

12.2 大边界的直观理解

12.3 数学背后的大边界分类（选修）

12.4 核函数1

12.5 核函数2

12.6 使用支持向量机

十三、聚类(Clustering)

13.1 无监督学习：简介

13.2 K-均值算法

13.3 优化目标

13.4 随机初始化

13.5 选择聚类数

十四、降维(Dimensionality Reduction)

14.1 动机一：数据压缩

14.2 动机二：数据可视化

14.3 主成分分析问题

14.4 主成分分析算法

14.5 选择主成分的数量

14.6 重建的压缩表示

14.7 主成分分析法的应用建议

十五、异常检测(Anomaly Detection)

15.1 问题的动机

15.2 高斯分布

15.3 算法

15.4 开发和评价一个异常检测系统

15.5 异常检测与监督学习对比

15.6 选择特征

15.7 多元高斯分布（选修）

15.8 使用多元高斯分布进行异常检测（选修）

十六、推荐系统(Recommender Systems)

16.1 问题形式化

16.2 基于内容的推荐系统

16.3 协同过滤

16.4 协同过滤算法

16.5 向量化：低秩矩阵分解

16.6 推行工作上的细节：均值归一化

十七、大规模机器学习(Large Scale Machine Learning)

17.1 大型数据集的学习

17.2 随机梯度下降法

17.3 小批量梯度下降

17.4 随机梯度下降收敛

17.5 在线学习

17.6 映射化简和数据并行

十八、应用实例：图片文字识别(Application Example: Photo OCR)

18.1 问题描述和流程图

18.2 滑动窗口

18.3 获取大量数据和人工数据

18.4 上限分析：哪部分管道的接下去做

十九、总结(Conclusion)

19.1 总结和致谢