简要介绍

解决的问题

在CNN未出现之前，图像分类等任务并不好解决，主要是存在以下两个问题：

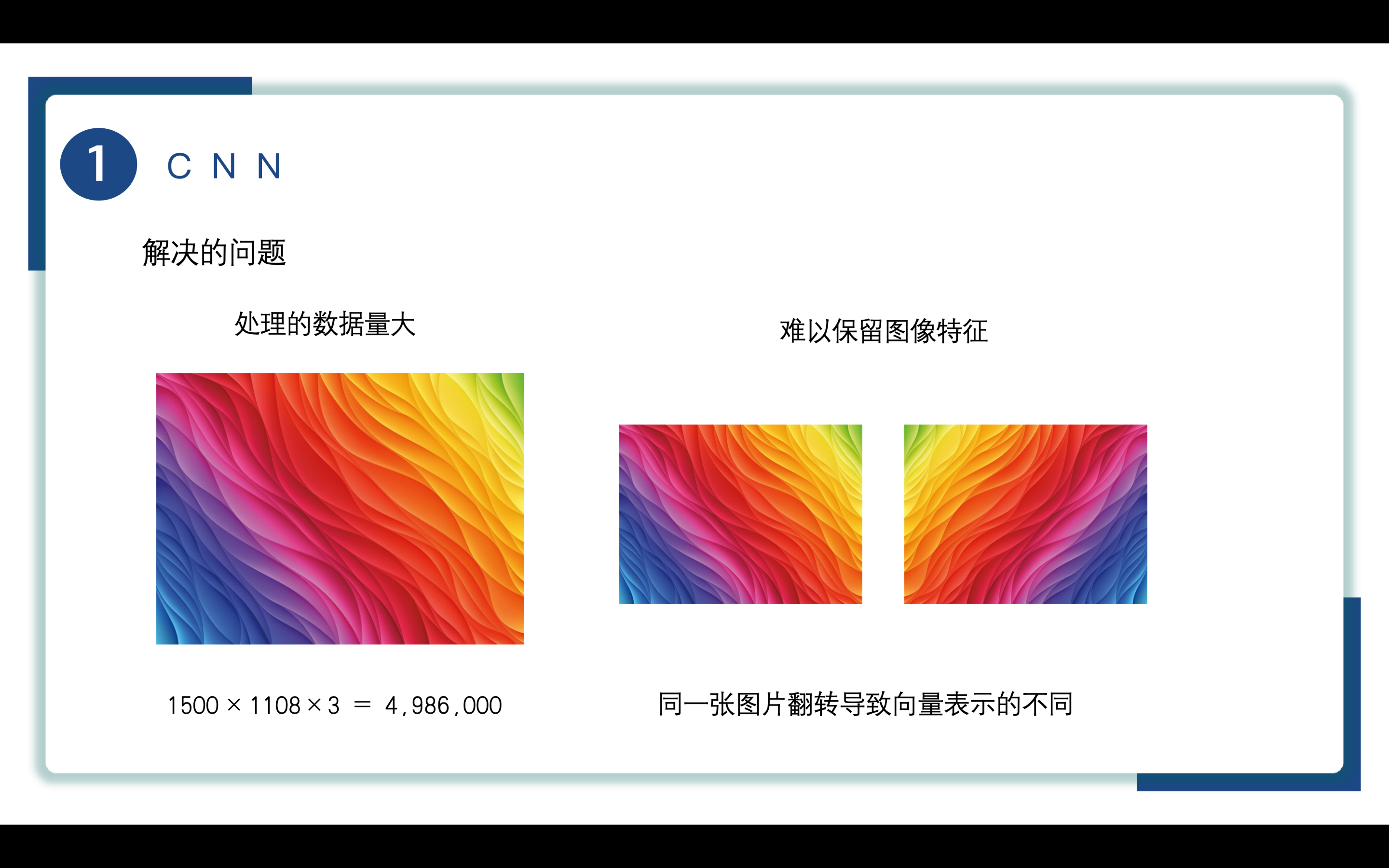
一是处理的数据量大，这里给出的彩色图片宽1500像素，高1108像素，RGB三通道，作为模型的输入的话会产生将近五百万个参数，对于计算机资源的要求会很高。且模型参数过多可能会导致的问题：训练慢、训练难（过拟合、欠拟合问题）

二是难以保留图像特征，同一张图片只是进行了左右翻转操作，但由于线性向量表示的方式不同，它们在向量空间中的表示也会有很大的差异，这是因为在向量表示中，每个像素的位置和颜色值都被编码为向量的一个维度，而左右翻转会改变像素的位置，从而导致向量表示中的差异。

解决这两个问题的核心是：

对数据进行降维/嵌入。在降低参数量的同时，尽可能保持原数据的数据特征。直观的理解是照片变模糊其实不太影响人类分辨出照片的内容。

使用视觉原理捕获图像数据中的数据特征。即在图像作反转、旋转、移动、缩放等操作时，机器都能像人类一样，认识到这些图片都是同一内容。

模型结构

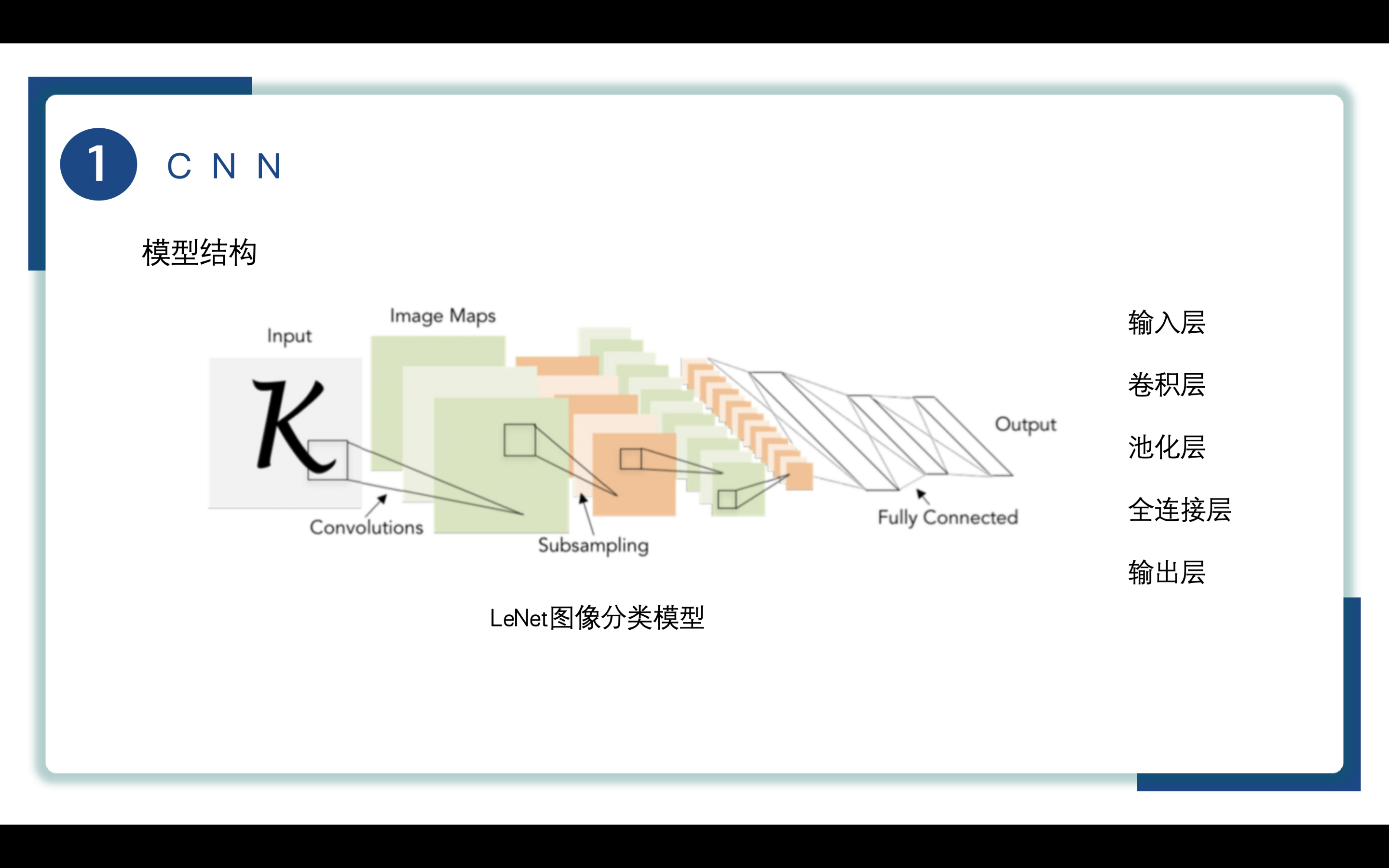
这里我们给出经典的CNN模型，也就是LeNet图像分类模型，该模型共有五层，接下来我们对除输入层输出层的另外几层进行解释。

卷积操作

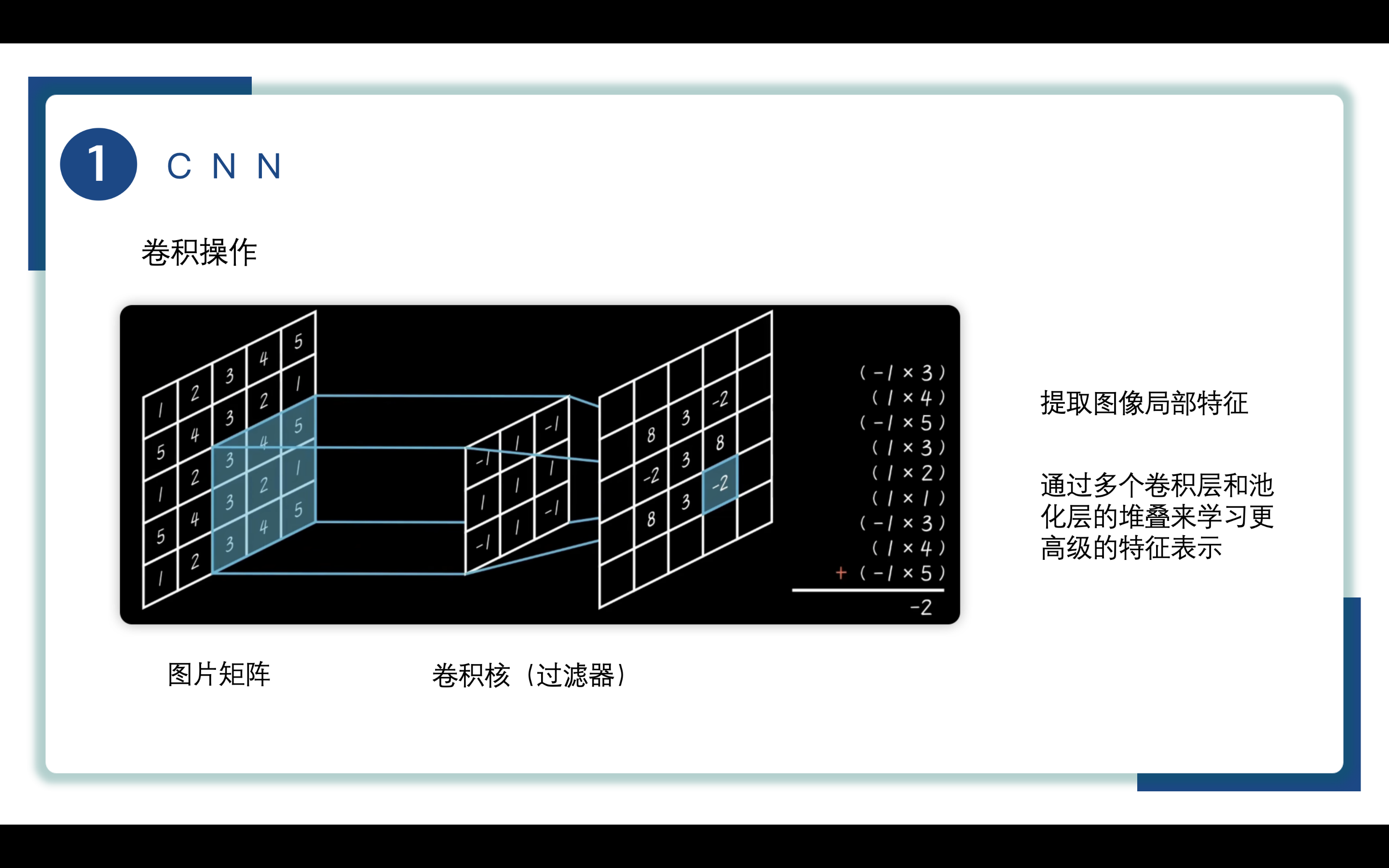
首先是卷积层，卷积层执行的是卷积操作，这也是CNN与简单的前馈神经网络最大的区别。

如图所示，这里进行的便是卷积操作，卷积层最重要的是卷积核，也可以称之为过滤器，卷积核是 CNN 中用来提取特征的关键部分，它通过对输入数据进行卷积操作，从而实现对不同特征的识别和抽取。 

卷积核的权重一开始随机初始化，之后通过反向传播进行学习和动态修正。

卷积核负责在输入数据上滑动并执行卷积运算，将局部特征与卷积核的权重相乘并求和，如图所示，从而提取出图像中的不同特征，如边缘、纹理等。

通过堆叠多个卷积层和池化层，可以提取出更加复杂和抽象的特征。因为随着网络深度的增加，每个卷积层可以提取出越来越复杂的特征。低层次的卷积核可能捕获像边缘和纹理这样的简单特征，而高层次的卷积核则可以捕获更复杂的特征，如物体的形状、部分、组合。

池化操作可以保留主要信息的同时减少数据量，有助于提高模型的鲁棒性和泛化能力。这种多层次的特征学习过程有助于提高网络的表达能力和分类准确度。

卷积核

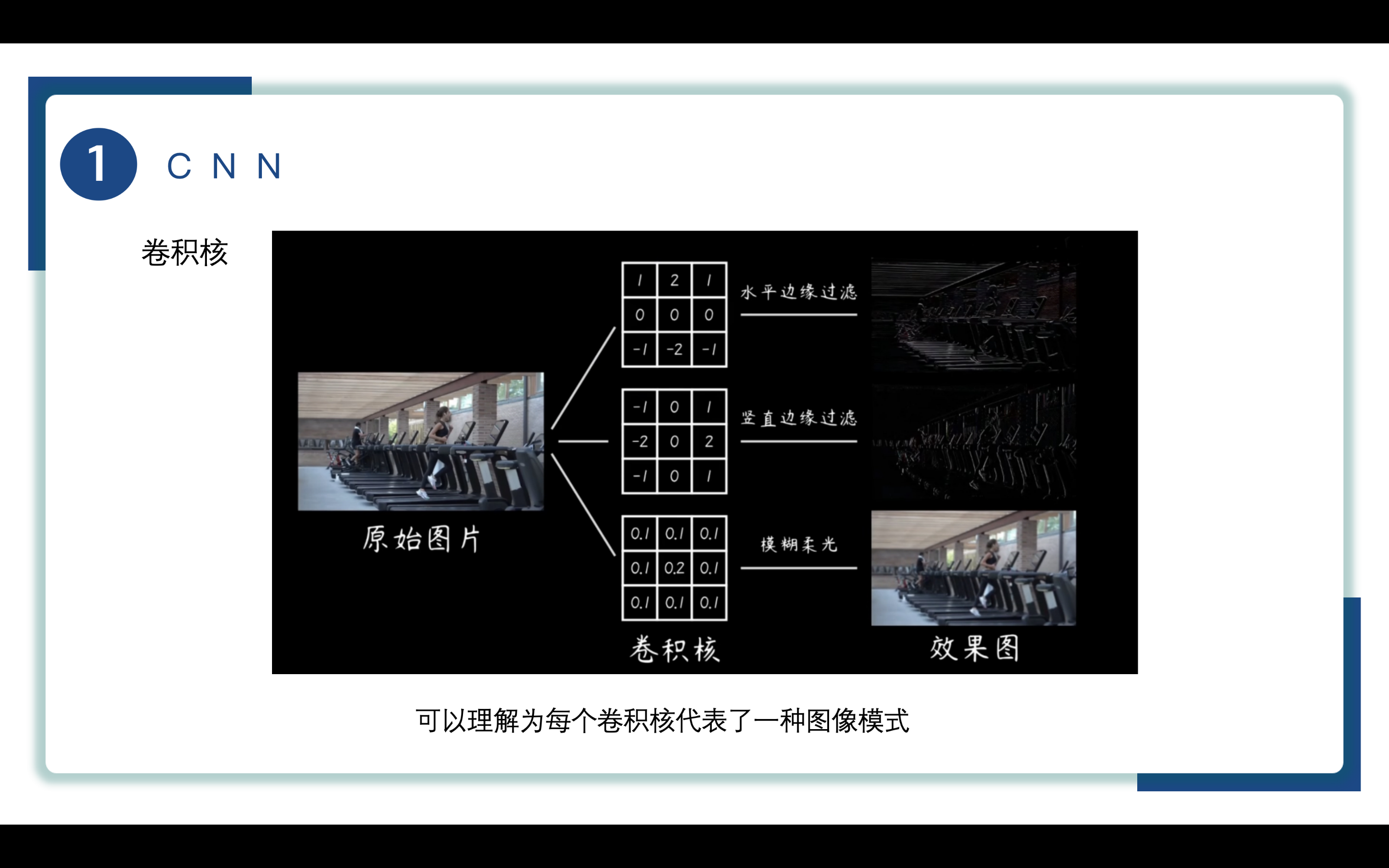
不同的卷积核能实现的提取特征功能也是不同的，可以理解为每一个卷积核代表了一种图像模式，如图所示，对于同一张图片采取不同的卷积核（过滤器），例如水平边缘过滤、竖直边缘过滤、模糊柔光，我们能够提取的输入数据的特征也是不同的，这些特征能够帮助我们进一步简化运算提高效率。通过利用卷积操作的参数共享、局部连接和稀疏交互等特性，可以实现对输入数据的高效特征提取和表示，为复杂模型的训练和推理提供了更快速和有效的方法。

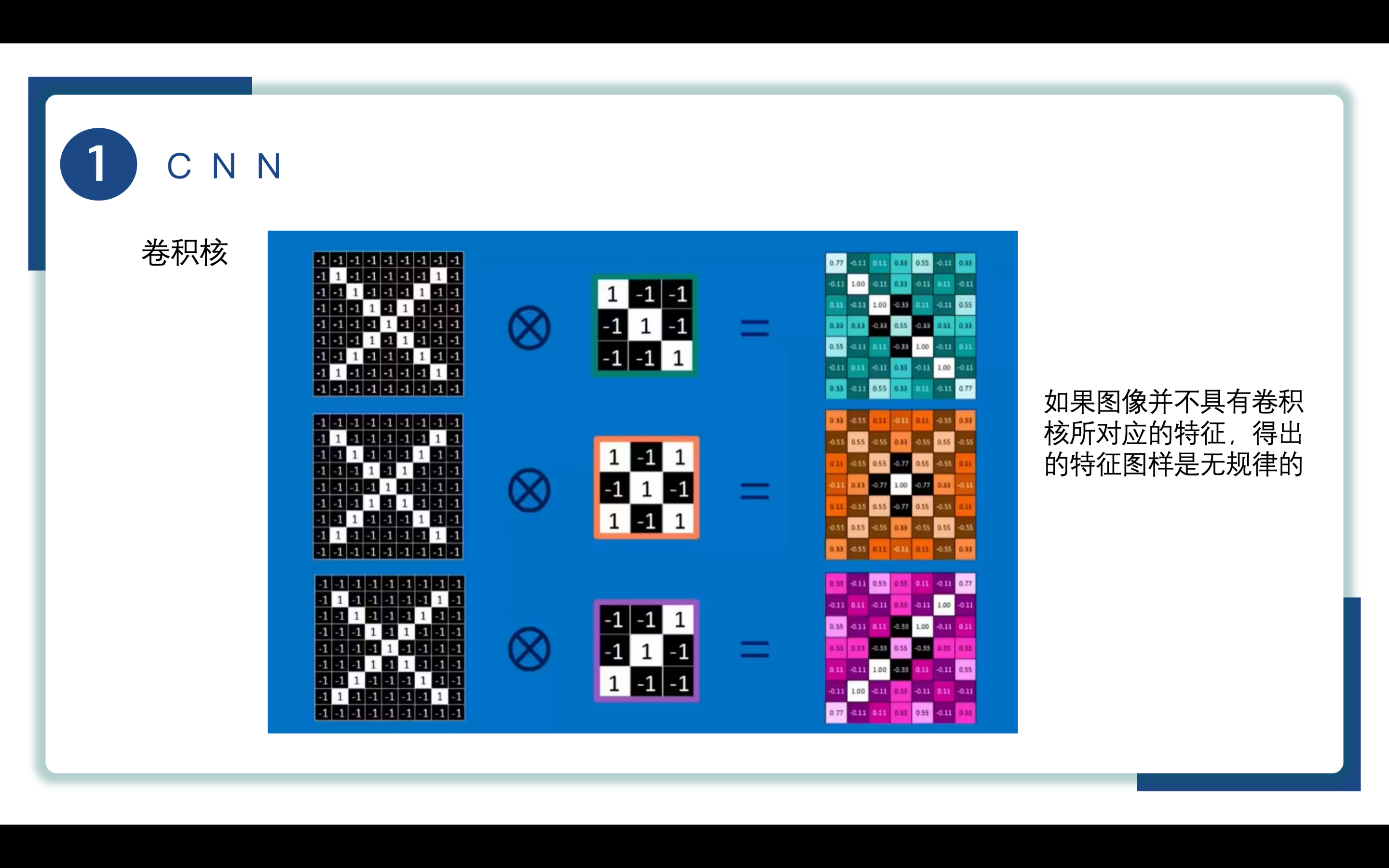
输入矩阵通过和不同卷积核的运算得出相应的结果，如果图像不具有该卷积核所对应的特征，则求出的特征图像，也就是feature map是无规律的。

feature map的无规律表现在几方面：

当输入图像没有与卷积核对应的特征模式，卷积操作可能无法有效地捕捉到有意义的特征信息，导致输出的 feature map 缺乏结构和有序性。

当输入图像与卷积核的预期特征不匹配时，卷积操作很可能会在输入图像上产生一些不明显或随机的响应，使得feature map 中的像素值没有明显的模式或规律，难以解释和理解。

在深度学习中，通过训练过程，网络中的卷积核会自动学习到对应于数据集中最具区分性和重要性的特征。如果某个卷积核对应的特征在输入数据中非常稀缺或不存在，该卷积核可能无法很好地进行特征提取，导致产生无规律的feature map。

所以需要通过反向传播BP来修正卷积核的权重，以让其能够准确地提取输入矩阵的局部特征。

激活函数

在卷积操作后通常会执行激活函数进行非线性变换。卷积操作本身是线性变换，多次堆叠的线性变换会导致整体仍然是线性的。引入非线性，打破网络的线性结构，使得网络可以学习到更丰富和复杂的特征表示，提高网络的表达能力。非线性激活函数的引入可以帮助网络更好地拟合复杂的数据分布，提高分类任务的准确性。

 先来讲一下常用的激活函数sigmoid，sigmoid函数在Logistic Regression中也存在，通过sigmoid函数使得模型的输出区间为【0，1】，这种特性使得Sigmoid函数在二分类问题中特别有用。

但是sigmoid函数不太适用于CNN，该函数存在指数运算，指数运算相比于普通运算代价更大，这会增加网络的计算开销，使得训练和推理的效率降低。

且Sigmoid函数的梯度在输入接近0或者很大时会趋近于0，导致梯度消失问题，这将影响反向传播过程中梯度的传播，使得网络难以学习。特别是在深层网络中，这种问题可能会变得非常严重。

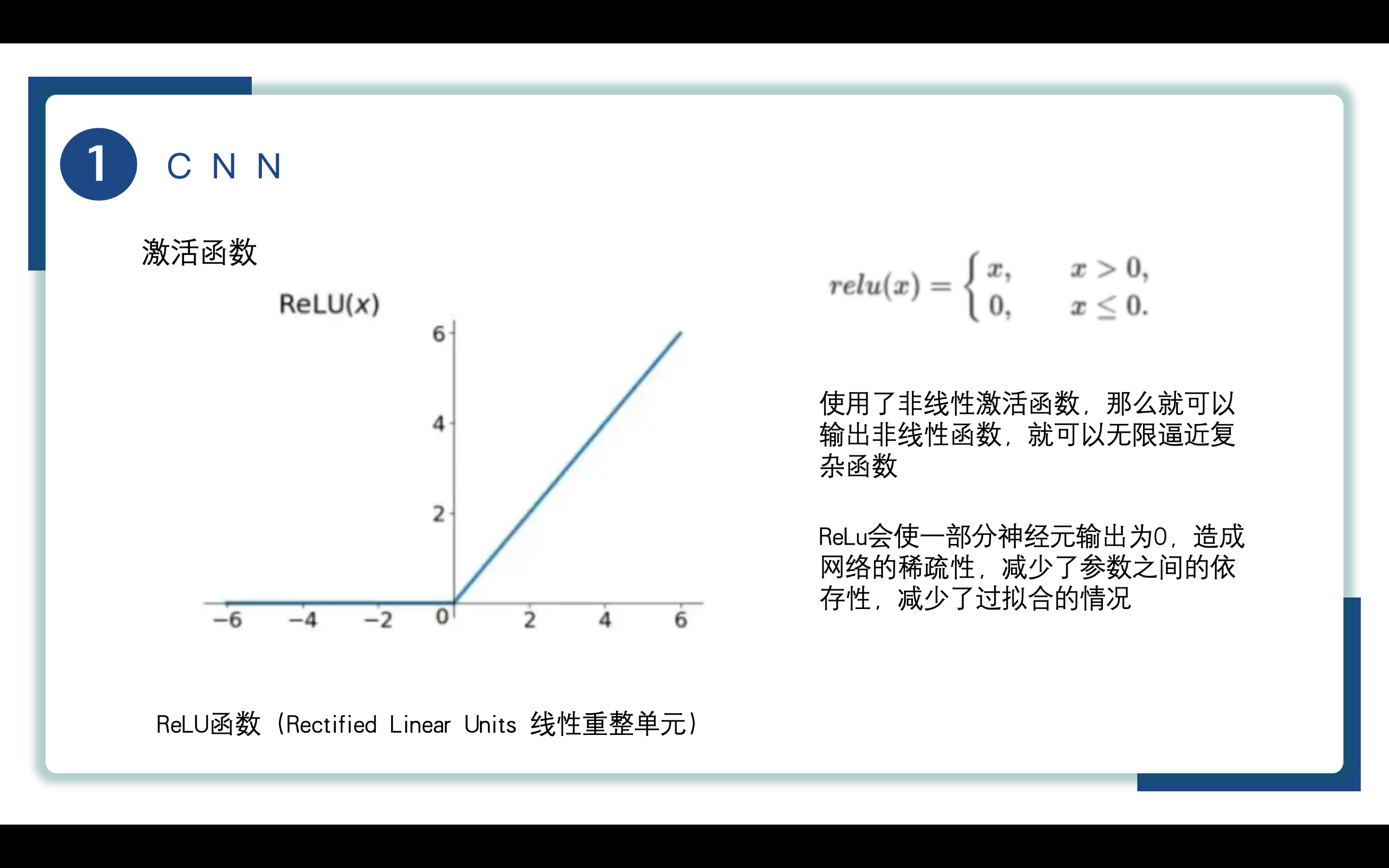
所以CNN使用ReLu（Rectified Linear Units 线性重整单元）函数，其表达式将小于等于0的数置0，大于0的数不做操作。

通过使用relu函数引入非线性变换，使得输出的非线性函数无限逼近复杂函数，拥有更强的表达能力和泛化能力。 

ReLu函数负数输入值映射为0的特性，这导致一部分神经元的输出为0，从而在一定程度上实现了网络的稀疏性。这种稀疏性带来了一些重要的优势，包括减少了参数之间的依存性、降低了过拟合的风险等。

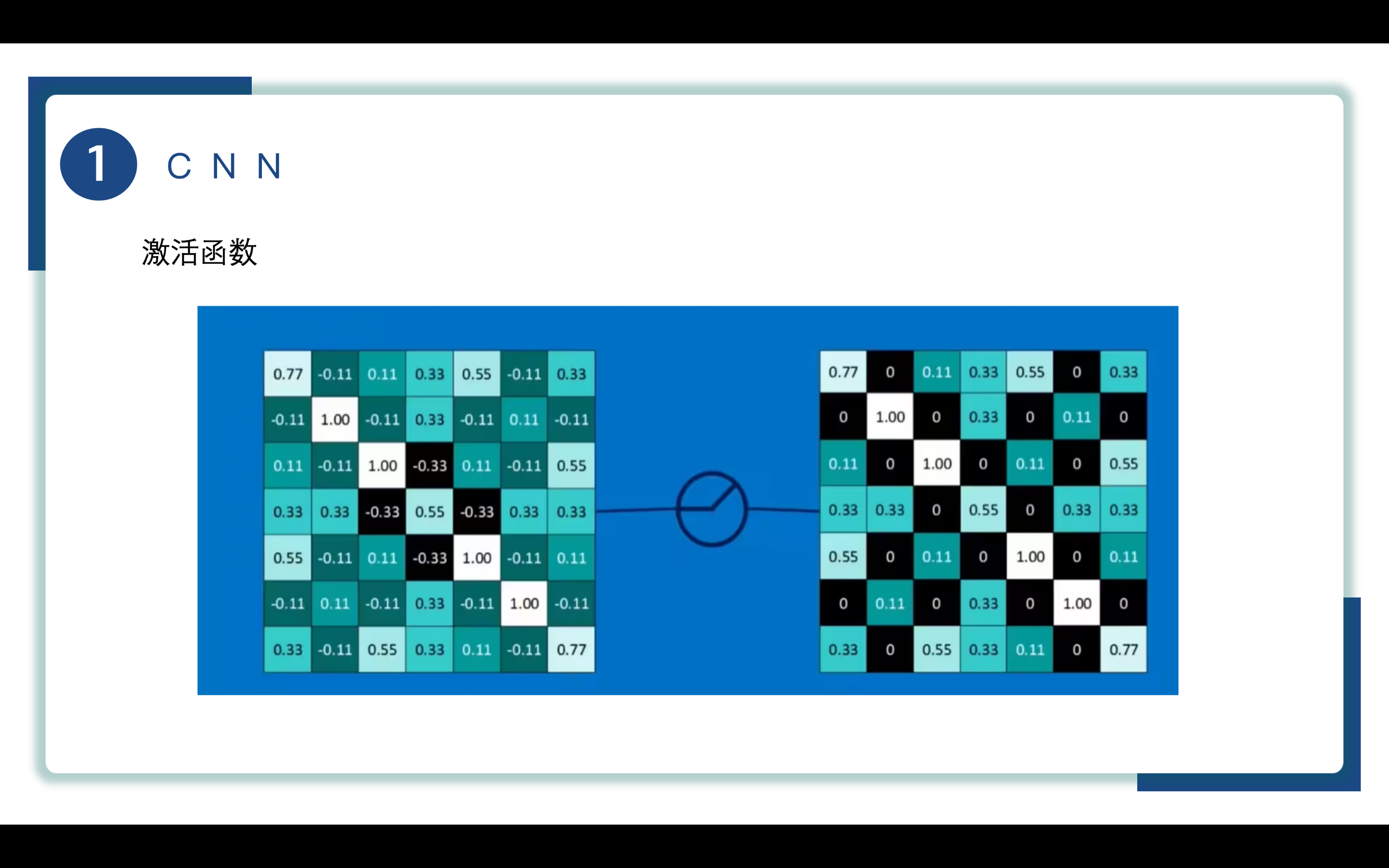
该图便是应用LeRu函数得到的结果，可以看到负数的部分都被置0，正数部分保持不变。

池化技术

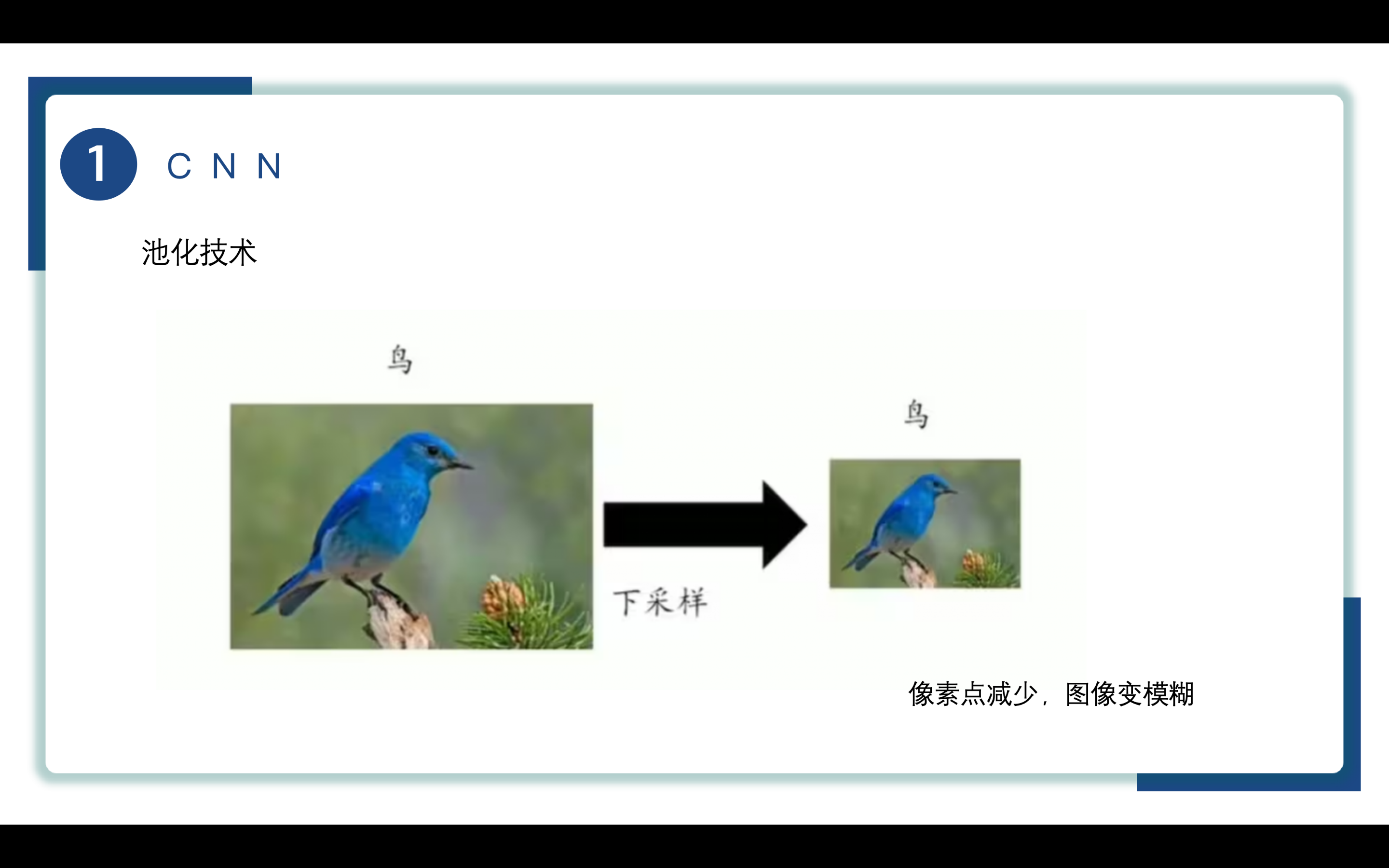
输入数据执行完池化操作，激活函数后便来到了池化层，池化层进行池化操作。

池化也被称为下采样。

如图所示，我们将图像进行横向和竖向像素的缩减，尽管图像的像素点减少，图像变模糊，但并不影响我们识别图像中的内容。

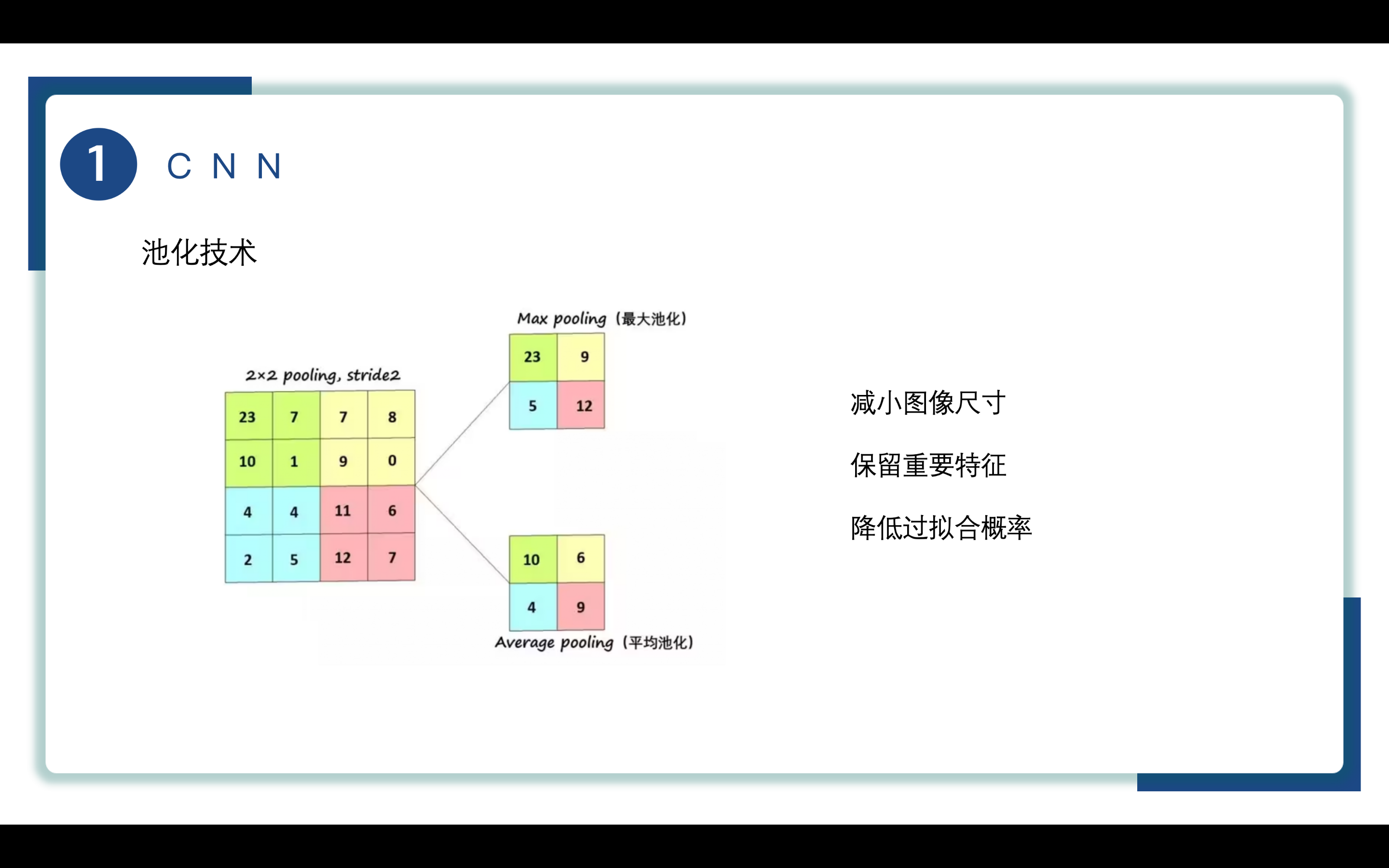
池化技术主要有两种：

最大池化：保留池化窗口中最大的元素

平均池化：池化窗口中所有元素求平均

显然通过池化技术 图像的尺寸被减小了，重要特征被保留了下来，池化操作可以提高模型的泛化能力，使得模型更容易推广到未见过的数据。这有助于减少模型在训练集上表现良好但在测试集上表现差的情况，从而降低过拟合概率。

具体的池化例子，这里采用的是最大池化技术，每个池化窗口中最大的元素被保留了下来

运算叠加

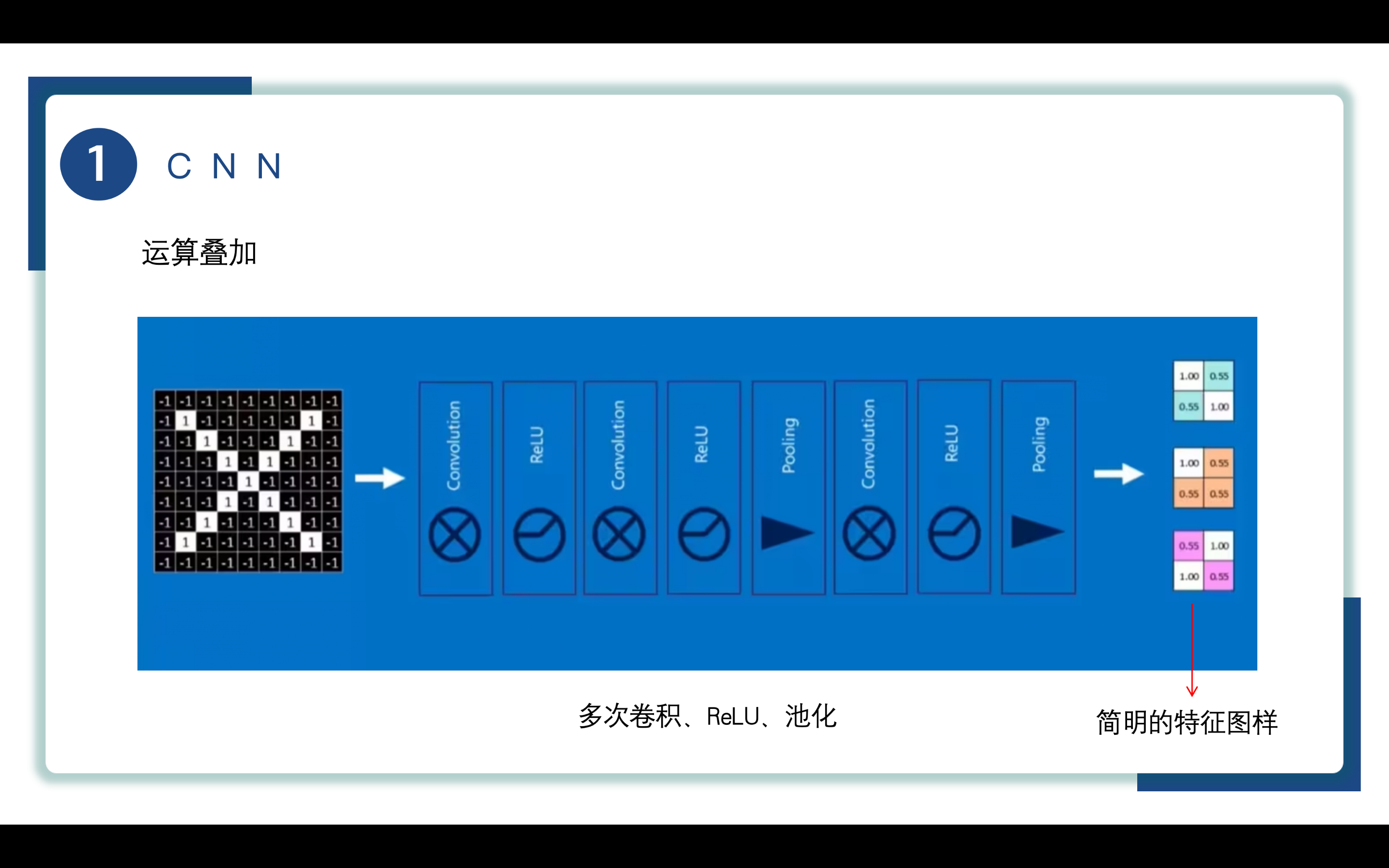
在实际运动CNN时，会出现多层运算的叠加，以此提取更加高级复杂的特征，提高网络的表达能力和分类准确度。如图所示，通过多次的卷积、Relu、池化操作后得到了简明的特征图样 feature map，相较于原本的输入矩阵，这些feature map参数量小且特征明显，适合当作输入数据用于最后结果的判定。

特征展开

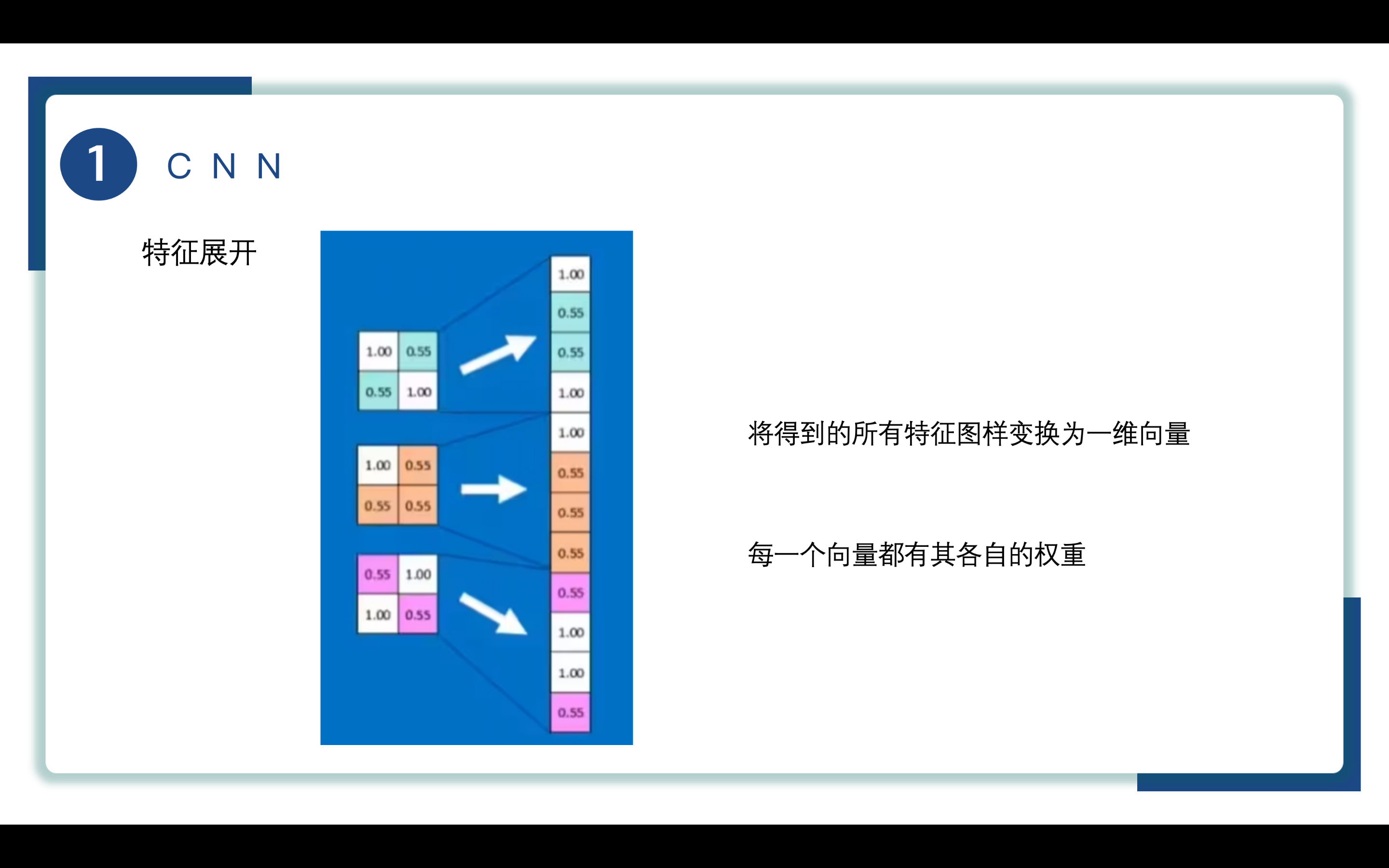
下一步将得到的所有特征图样展开变换为一维向量，每一个向量都有其各自的权重进行运算

全连接

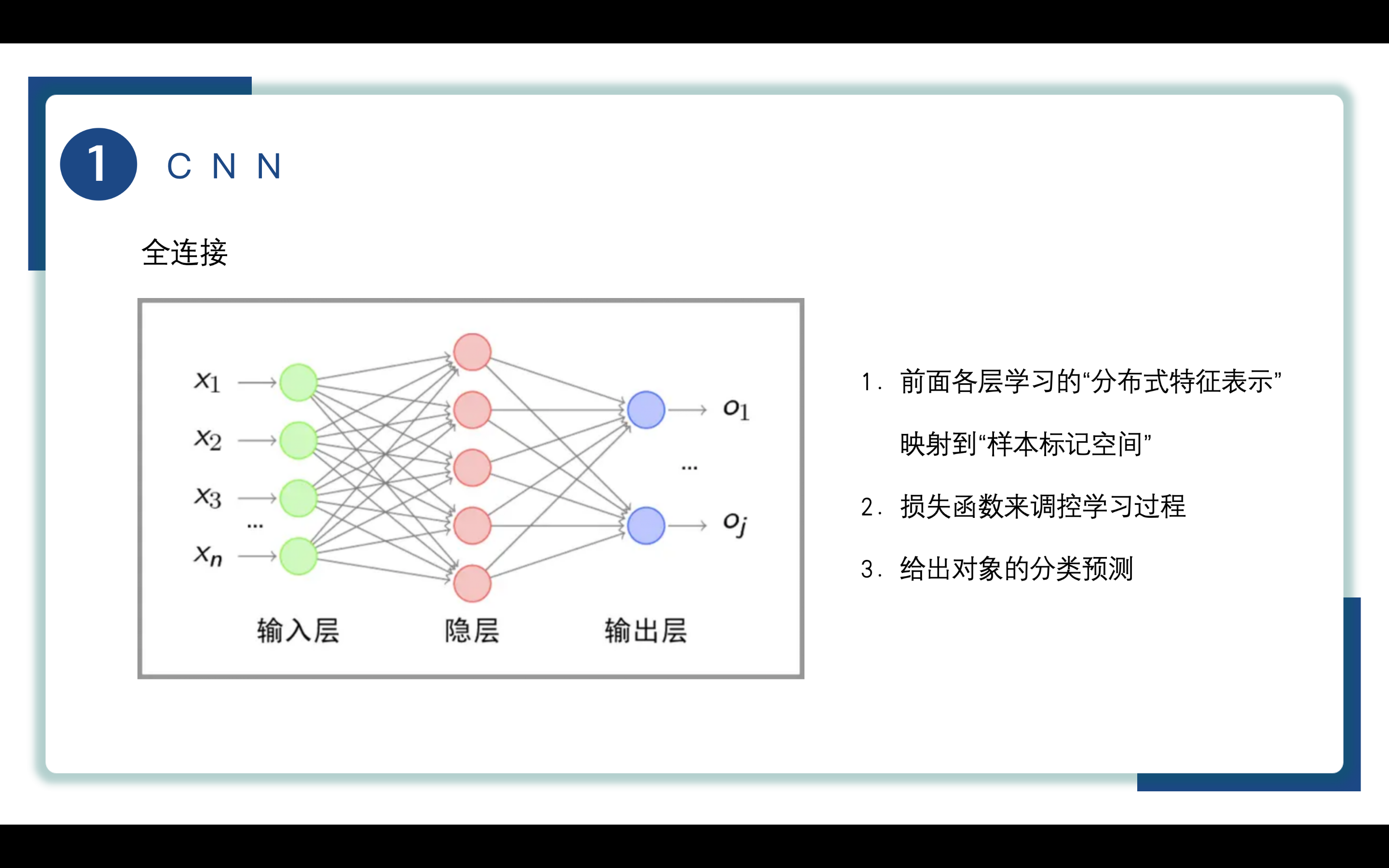
完成上述操作后来到了全连接层，该层执行全连接操作，全连接层可以使用softmax或者逻辑回归作为输出层的激活函数，用于实现多分类或二分类任务。

全连接层是一种基本的神经网络结构，分别是input layer hidden layer output layer ，将输入的feature map得出对象的分类结果。

通过损失函数来调控学习过程，更新模型权重以达到更高的准确率和更好的性能。

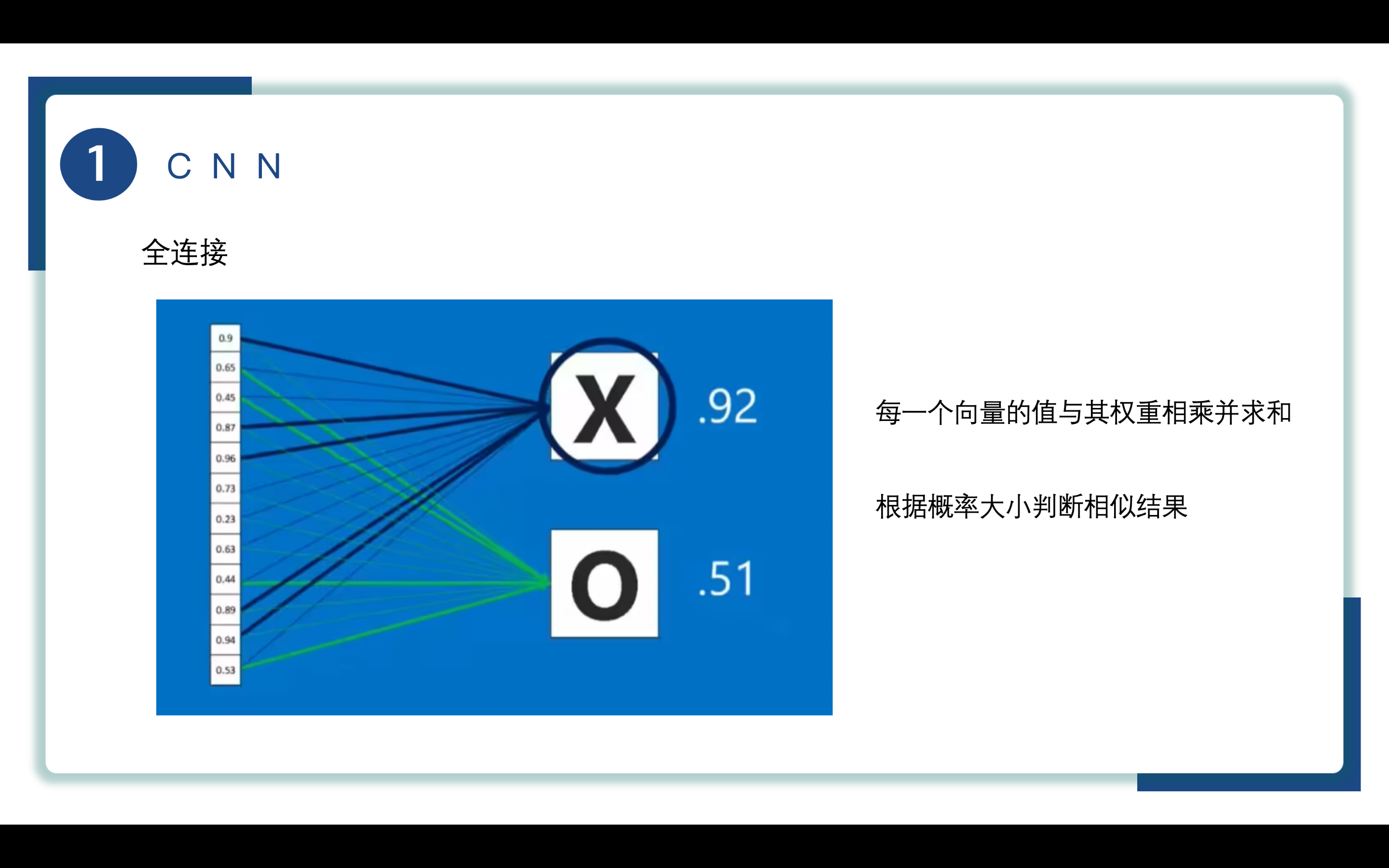
每一个向量的值与其权重相乘并求和，根据概率大小判断相似结果，此图表明给出的特征和权重运算的结果更符合X这个类别。

整体流程

讲完了各层的作用，来对总体流程做个总结，这里还是以LeNet模型为例。

介绍完CNN，我们可以对先前的两个存在的问题作出解释：

在CNN中，卷积核通过滑动窗口的方式在输入图像上提取特征。由于卷积核在图像上进行平移操作，所以当图像进行水平翻转后，提取到的特征仍然会保持不变。换句话说，CNN在学习过程中会学习到与物体形状、纹理等相关的局部特征，而这些特征并不受图像的镜像变换影响。这解决了无法很好保留图像特征的问题。

通过一系列的特征提取过程，简化参数，降低参数量，解决处理的数据量大的问题。

参数选择

似乎还没有对参数进行解释，在CNN中可学习的参数，包括卷积层和全连接层的权重参数、偏置项以及批量归一化等参数是通过反向传播修正的。

而池化窗口的大小和步长、卷积核的大小则是超参数，由人为指定。

反向传播

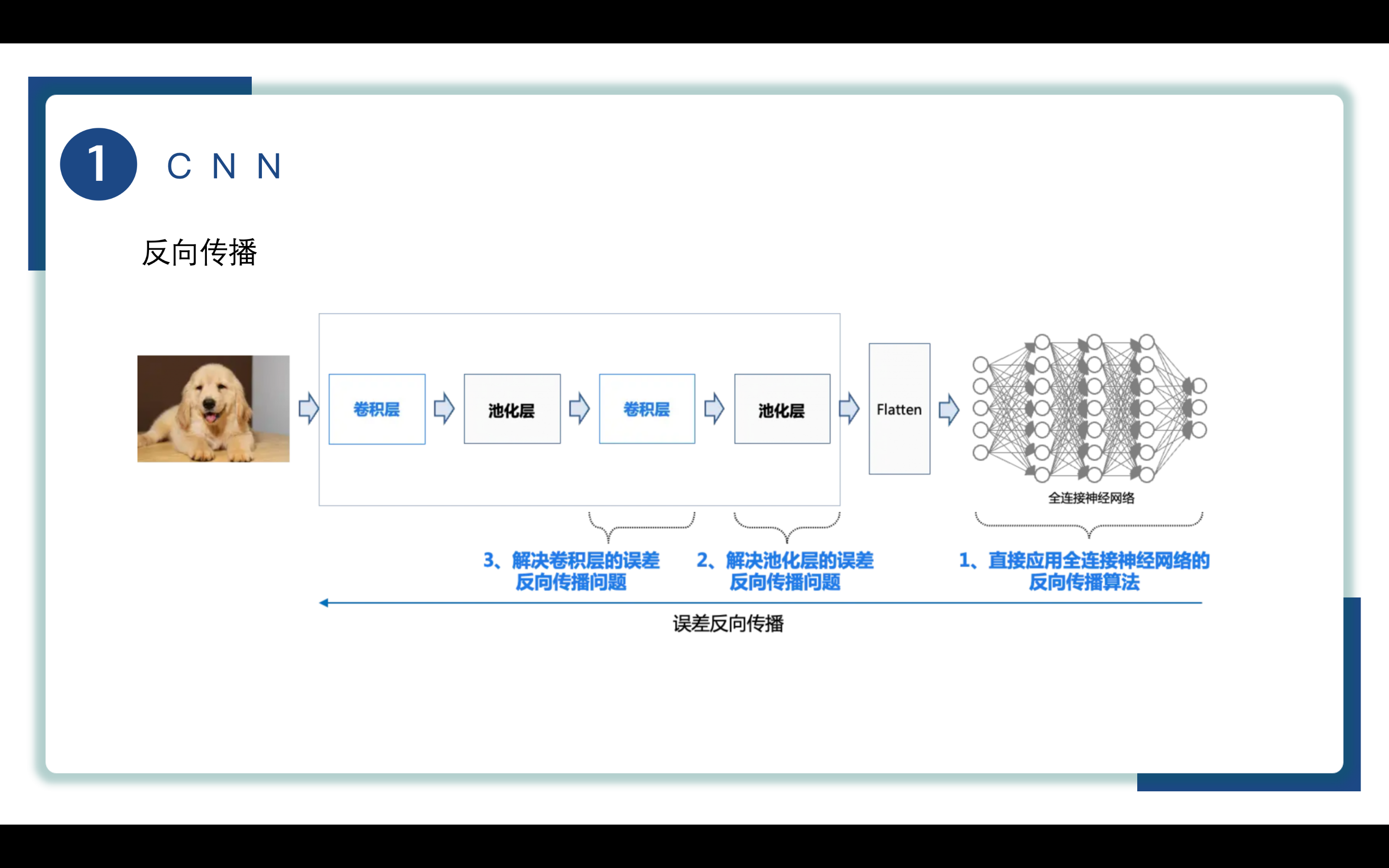
再讲一下CNN的反向传播BP

我们需要解决三部分的反向传播问题

全连接层则直接应用全连接神经网络的反向传播算法

池化层的池化操作是固定操作，没有学习参数，将误差向上传即可

卷积层的反向传播则比较复杂，CNN的卷积层在反向传播中，首先从输出层开始计算误差梯度。误差通过卷积核进行反向传播，与输入数据进行卷积操作得到输入数据的梯度。同时，将误差与卷积核进行翻转、旋转操作后再进行卷积得到卷积核参数的梯度。这些梯度用于更新卷积核参数和偏置项，以优化网络参数，在训练过程中不断调整权重，提高模型性能和泛化能力。

卷积层的BP涉及到卷积和多个feature map的运算，复杂性较高。

实际应用

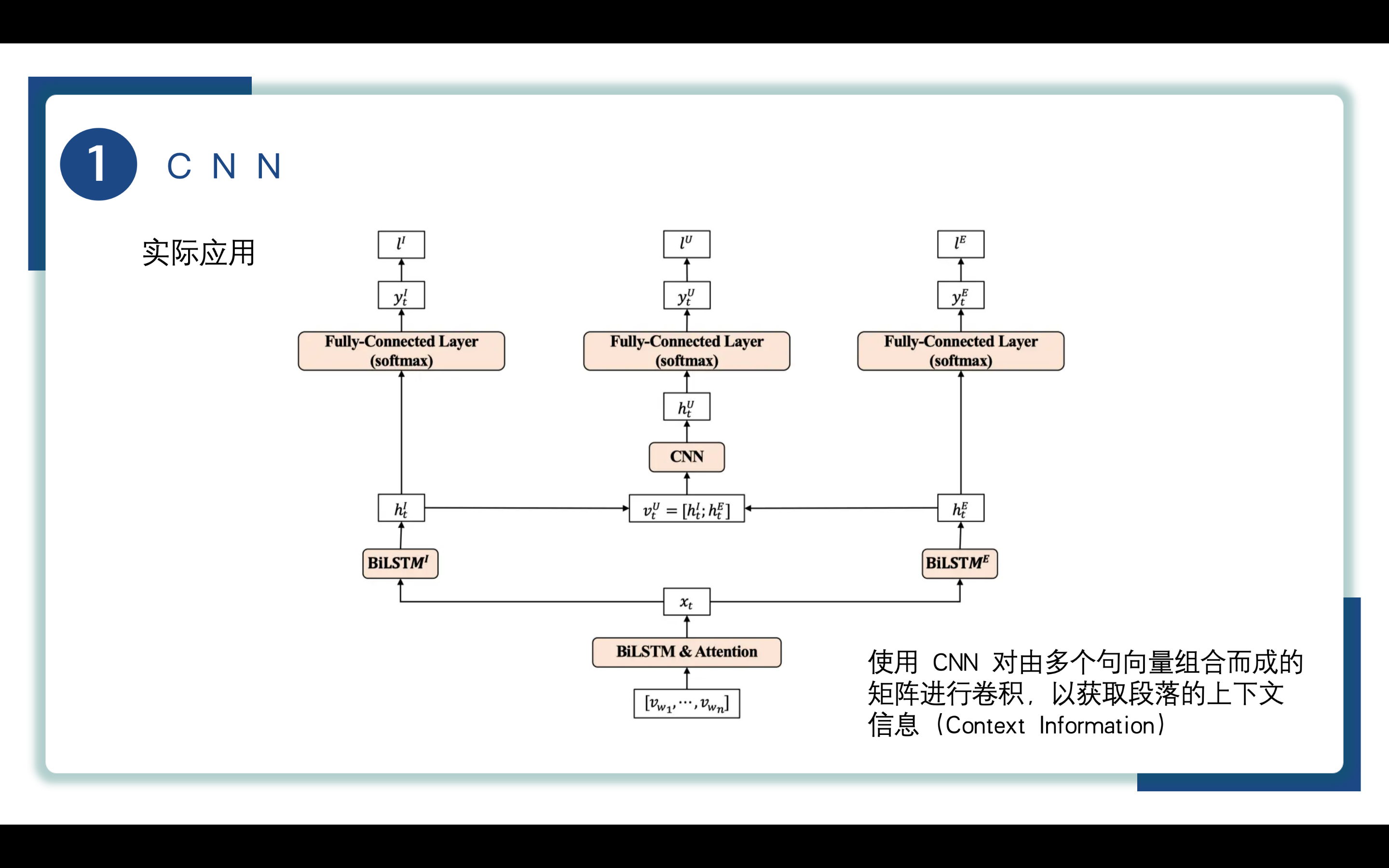
最后来讲一下CNN的实际应用，包括CV方面的图像分类、目标检测、人脸识别。

CNN在NLP方面也有应用，该论文使用 CNN 对由多个句向量组合而成的矩阵进行卷积，以获取段落的上下文信息（Context Information）。