Leetcode题目链接：70. 爬楼梯

题目描述：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

解题思路：

DP解题五部曲-----源于B站UP代码随想录

• dp数组的定义及下标：dp数组用于记录到达第 i 级台阶的方法个数，即到达第 i 级台阶总共有dp[ i ]种方法

• 递推公式：dp[i] = dp[i - 2] + dp[i - 1]，到达第 i 级台阶的方法个数受到前 i - 1 和 i - 2 级台阶方法的影响

  • 以第 3 级台阶为例子， 到达第一级台阶有 1 种方法，从第 1 级台阶到第 3 级台阶只有一种方法（有且仅有从 1 级台阶爬 2 个台阶上到第 3 级台阶）

  • 到达第二级台阶有两种方法，从第 2 级台阶到第 3 级台阶只有一种方法（有且仅有从 2 级台阶爬 1 个台阶上到第 3 级台阶）

  • 以此类推的出了上面的递推公式

• dp数组初始化：dp[ 1 ] = 1，dp[ 2 ] = 2;

• 遍历顺序：由于到达第 i 级台阶的方法个数受到前 i - 1 和 i - 2 级台阶方法的影响，需要从前往后遍历。

• 打印dp数组

我的答案：

class Solution {
public:
    int climbStairs(int n) {
        int dp[n+1];
        if(n == 1)return 1;
        if(n == 2)return 2;
        dp[1] = 1;dp[2] = 2;
        for(int i = 3;i <= n;i++){
            dp[i] = dp[i - 2] + dp[i - 1];
        }
        return dp[n];
    }
};

提交结果：

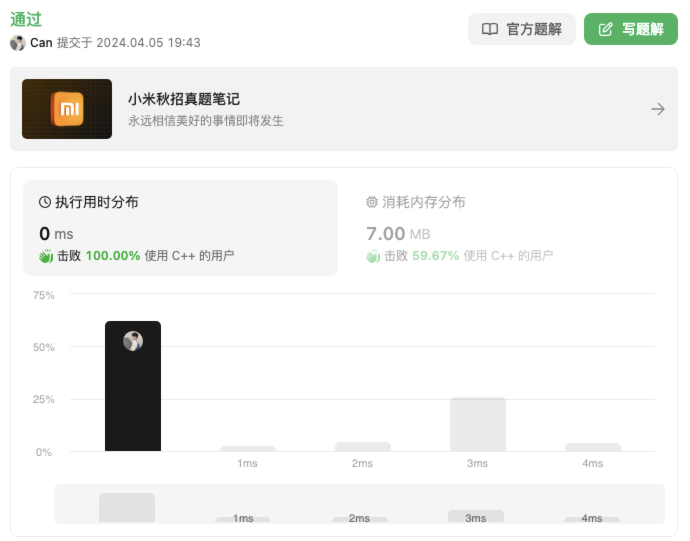
官方答案：

class Solution {
public:
    int climbStairs(int n) {
        int p = 0, q = 0, r = 1;
        for (int i = 1; i <= n; ++i) {
            p = q; 
            q = r; 
            r = p + q;
        }
        return r;
    }
};

作者：力扣官方题解
链接：https://leetcode.cn/problems/climbing-stairs/solutions/286022/pa-lou-ti-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

偷鸡答案：

def climbStairs(self, n: int) -> int:
    arr = [0, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296, 433494437, 701408733, 1134903170, 1836311903] 
    return arr[n]