论文：Isolation Forest.pdf（ICDM 2008）

背景

首先讲一下孤立森林算法提出的背景。

异常检测的应用场景对算法的检测性能和执行速度要求很高。

传统的检测算法需要构建实例模型以判断是否是异常，这使得模型存在过度关注正常示例导致实际识别效果欠佳和高计算复杂度限制数据运算维度的问题。

实际数据可能存在分布不均或噪声的情况，但好在异常通常是few and different的，是少和不同的，这使得我们能够容易地划分异常。

动机

基于以上提到的背景，作者提出了一种新的异常检测方法，即iForest 孤立森林。该算法充分利用了异常存在的两种性质，即异常是数据实例的少部分且拥有与正常实例所不同的属性值。具体的思路是使用树形结构（iTree）以隔离每个实例，异常点靠近树根，正常点远离树根，即正常点拥有较大的深度。

iForest的一次运行会通常包含多个iTree的构建执行。

方法

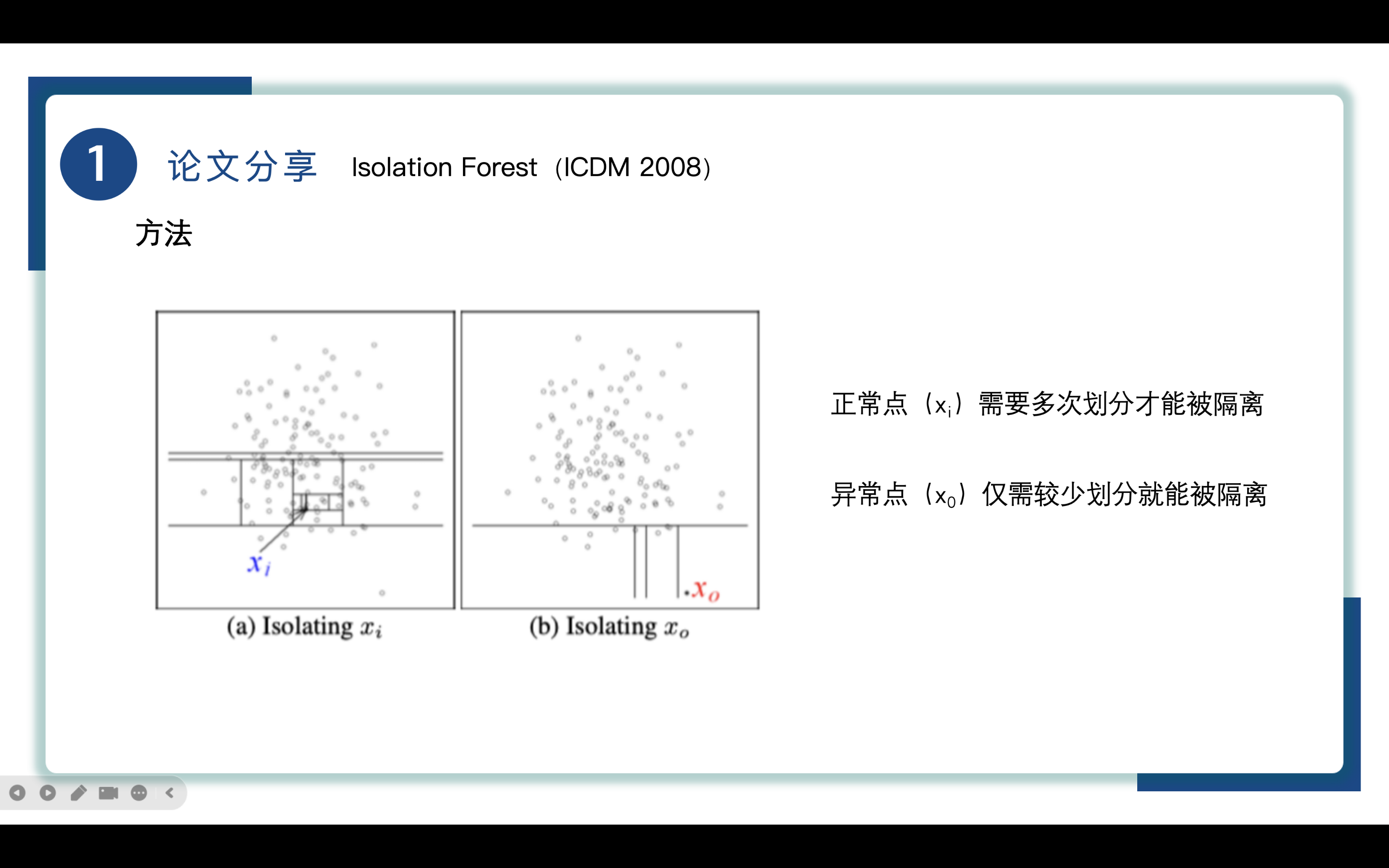
先来解释一下Isolation隔离的概念。

如图所示，我们使用直线对实例进行划分，每个点我们认为是一个实例，划分实例是递归执行的，直到所有的实例都被隔离开，拥有较少划分次数的实例更可能是异常点。

由于异常点通常在早期的划分中就被隔离出来了，这使得异常点在树中靠近根结点，拥有较短的路径长度，如图中的x0点。

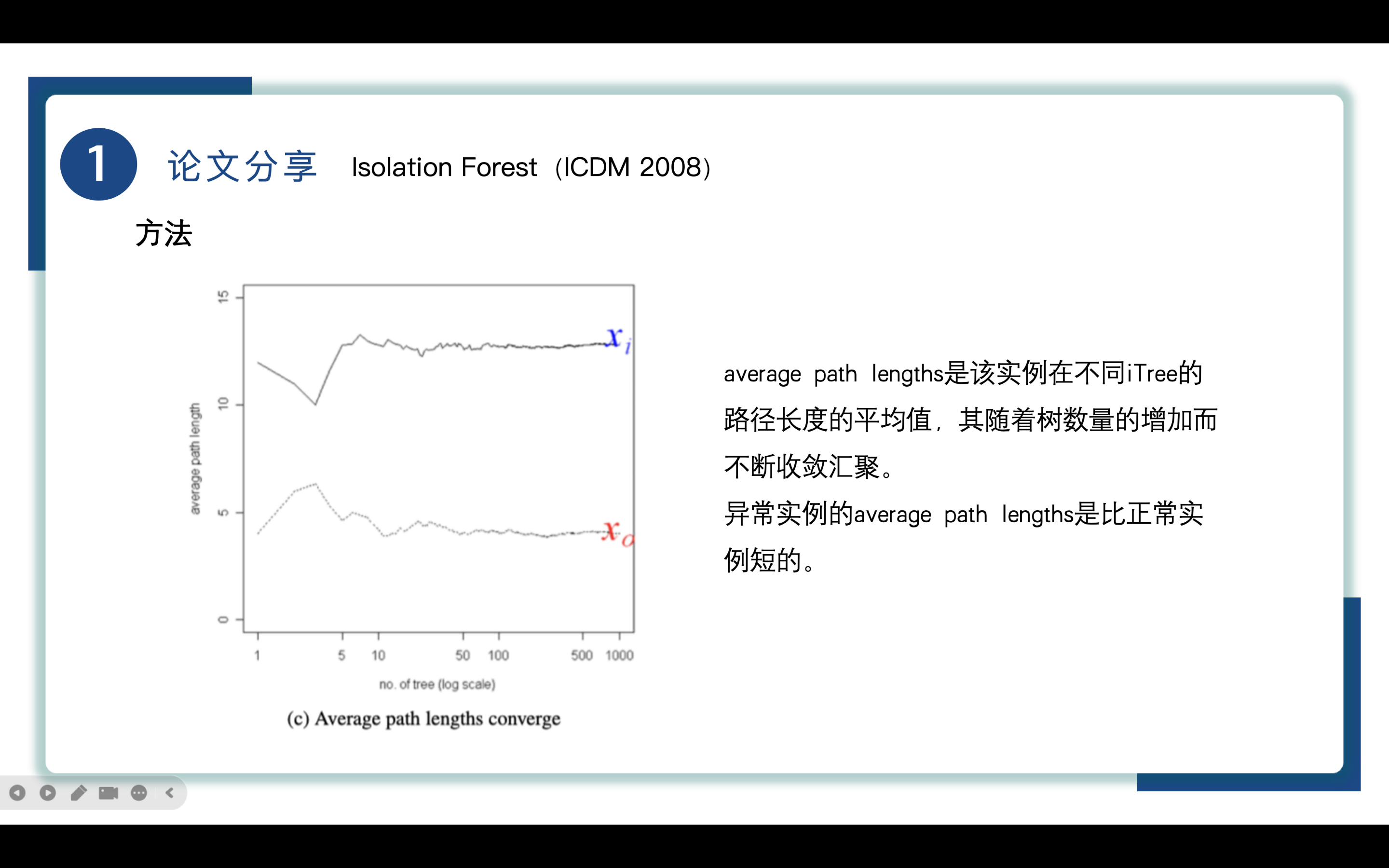
由此作者提出了一个average path lengths 平均路径长度的概念，average path lengths是该实例在不同iTree的路径长度的平均值，其随着树数量的增加而不断收敛汇聚。在一次iForest的执行过程中，实际上包括了多个iTree的构建和执行。每棵iTree都是通过随机选择特征和切分点来构建的，最终形成的树结构用于隔离数据实例，以此来计算对应实例的average path lengths来有效地评估数据实例的异常性。

图中x轴是iTree的数量，y是平均路径长度，随着iTree数量的增加，平均路径长度收敛，在本文中100也被用作设置iTree的数量。

从图中我们也能直到异常实例x0的平均路径长度是比正常实例xi短的，这意味着该实例被隔离的难度是小于正常实例的。

接下来作者又给出了几个关键指标的定义。

Path Length h(x) 从根结点到终端结点x之间经过的边的数量，刚才我们提到的average path lengths就是h(x)取平均的到的。

c(n)是给定n后得到的h(x)平均值，用于h(x)的归一化，其中，

H(n) 是第 n 个调和数，用来估计在随机分裂情况下样本的平均路径长度，这个计算公式是二叉查找树BST的失败查找长度的计算方法借鉴过来的。

接着提出本文中最重要的一个指标 anomaly score 异常分数，它的公式如公式（2）所示，

其中E(h(x))是h(x)的平均值，实际就是我们之前提到的average path lengths。

当E(h(x))接近于0时,即x的路径长度很短，则s接近于1，当E(h(x))接近于n - 1时，x的路径长度很长，则s接近于0.

查看计算出的score分数值，若接近1则必定是异常点，若小于0.5被认为是正常点，所有实例均靠近0。5则所有实例没有明显异常。

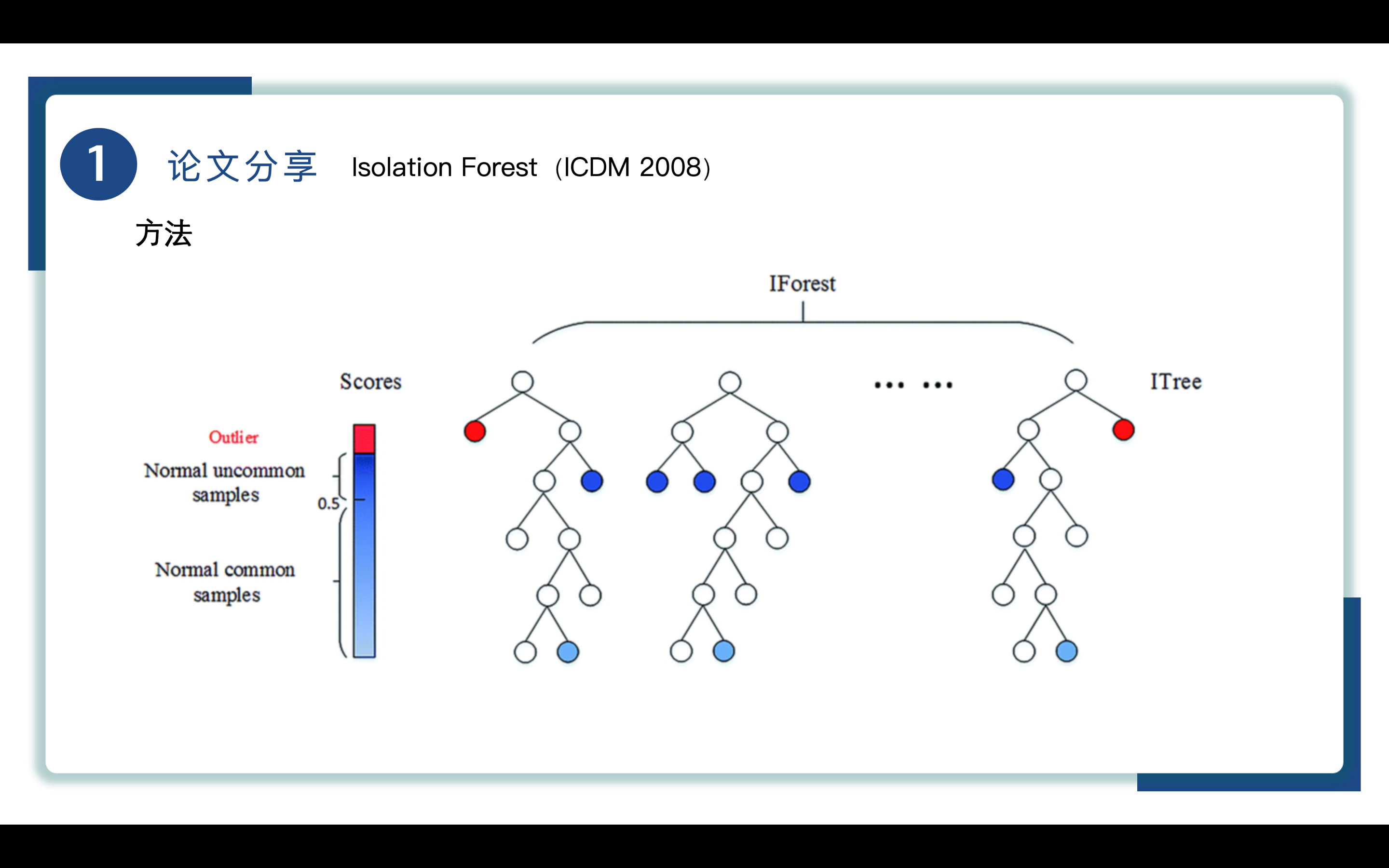
这张图解释了iForest的执行过程，iForest递归执行划分的过程能够被树形结构所表示。每次划分其实就像二叉树分支的生长，iTree通过随机选择特征和随机选择切分值来进行划分，这种划分方式使得每个节点都可以分成两个子节点，从而形成树的结构，可以看到通过二叉树分支的生长，我们逐渐将异常点剥离出来，靠近树根的点路径长度短，异常得分也高，被认为是outlier即异常。我们也可以将孤立森林算法形象理解为剥笋的过程，一般外皮是不可食用的，我们将其看作异常，对笋进行进一步地剥离，当外皮剥离到一定程度时就不需要再剥离了，我们通常认为未被剥离的部分是可食用的，将其看作正常点，在异常检测的过程中我们更关注笋的外皮也就是异常，对笋的内部不过多关注，这也就意味着实际执行过程中树并不会太高，这大大降低了运算复杂度。

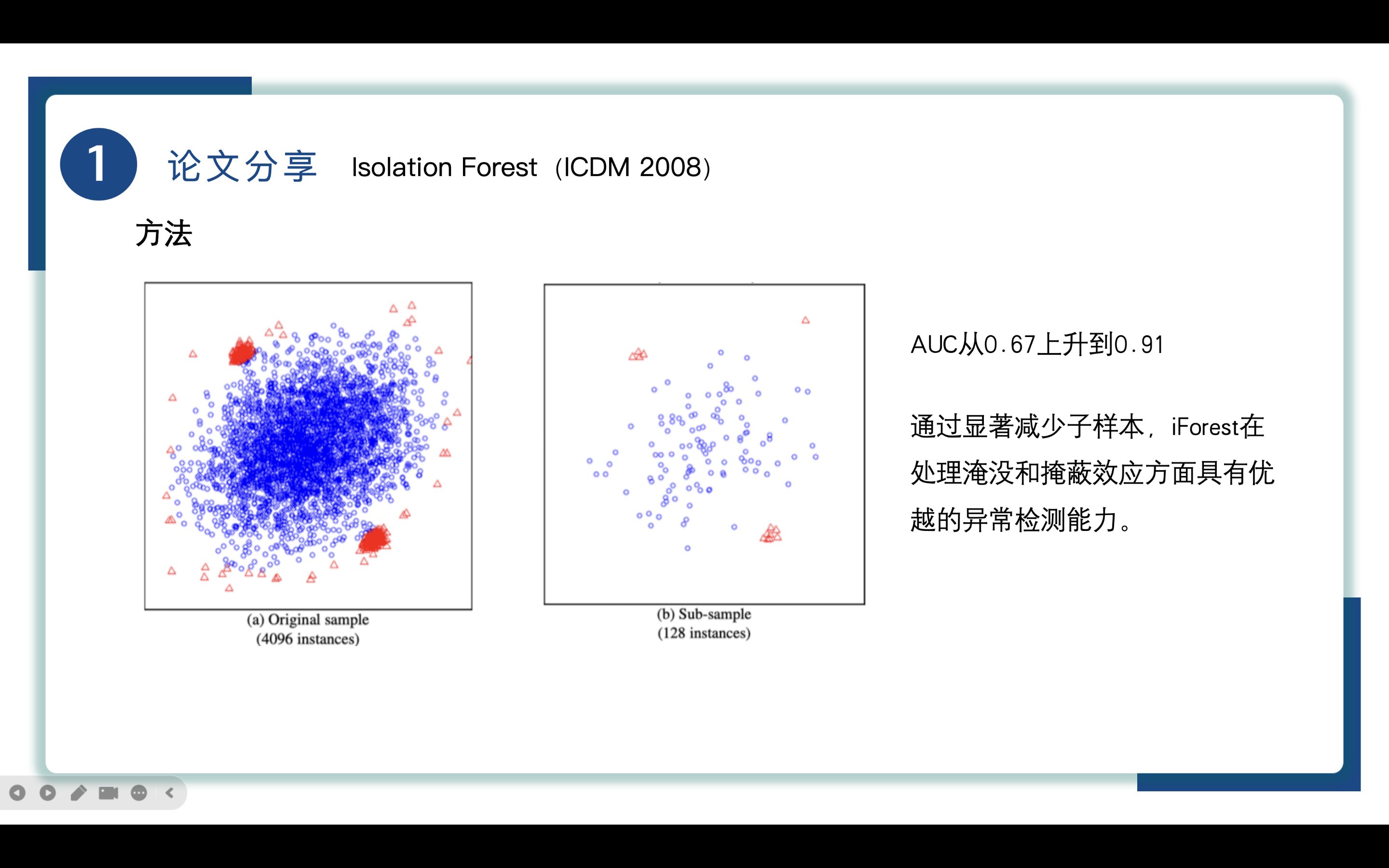
AUC（Area Under the Curve）是用于评估模型性能的重要指标，特别是在异常检测任务中。AUC的计算基于ROC曲线（Receiver Operating Characteristic Curve），它展示了不同阈值下模型的真阳性率（TPR）与假阳性率（FPR）之间的关系。通过计算AUC可以判断模型在识别异常值方面的能力，AUC值越高，表示模型的性能越好。

如图所示，(a图)存在淹没和掩蔽两个问题，淹没是指在正常实例过分靠近异常时将正常实例误认为异常，掩蔽当异常集群很大时划分单个异常的成本增大，而通过减少子样本的大小，AUC从0.67提高到了0.91，证明了iForest在处理淹没和掩蔽效应方面的优势。

iForest算法

目的：构建多棵iTree来形成一个孤立森林，用于检测数据中的异常值

输入：数据集 X，树的数量 t，每棵树的样本子集大小 ψ

输出：iTree的集合

具体步骤：

1.随机选择 ψ （普西）个样本，构建一棵iTree

2.重复上述过程 t 次，得到 t棵iTree

iTree算法

目的：构建一棵隔离树，用于隔离数据集中的样本

输入：样本子集 X，当前树的深度 e，最大树深度 l

输出：一棵iTree

过程：

如果 e≥l或 X′中的样本数小于等于1，则返回当前节点

随机选择一个特征 q 和一个分割点 p

根据 p将样本分为左右子节点

递归地对左右子节点构建iTree

PathLength算法

目的：计算样本在iTree中的路径长度，用于评估样本的异常性

输入：样本 x，iTree T,当前路径长度e

输出：样本 x的路径长度 h(x)

过程：

从根节点开始，沿着树的分裂路径遍历，直到到达叶节点

记录经过的边数，即为路径长度 h(x)

实验

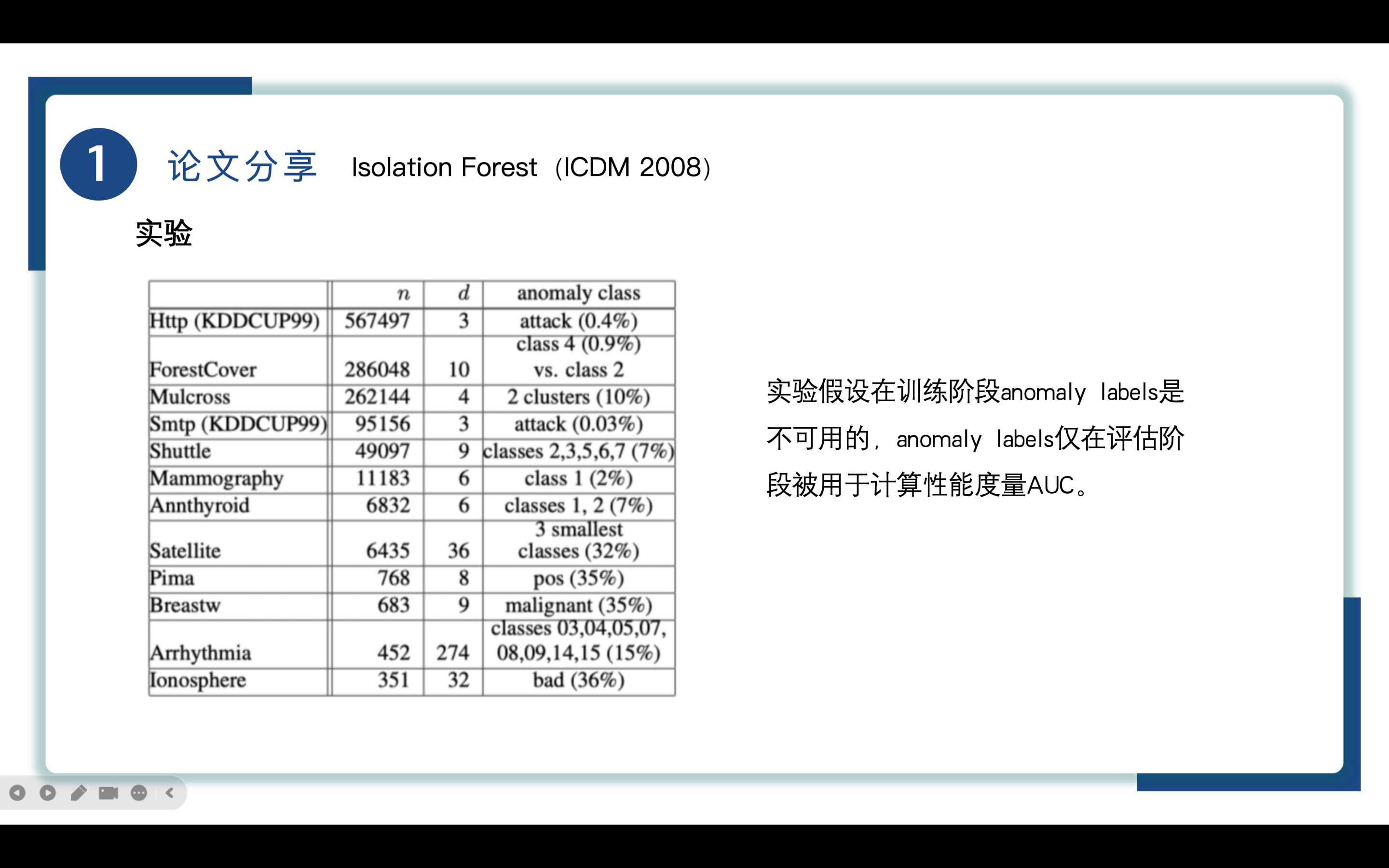
来到实验部分，作者在不同的数据集上比较iForest和ORCA、LOF、RF，数据集如图所示，实验假设在训练阶段anomaly labels是不可用的，anomaly labels仅在评估阶段被用于计算性能度量AUC。

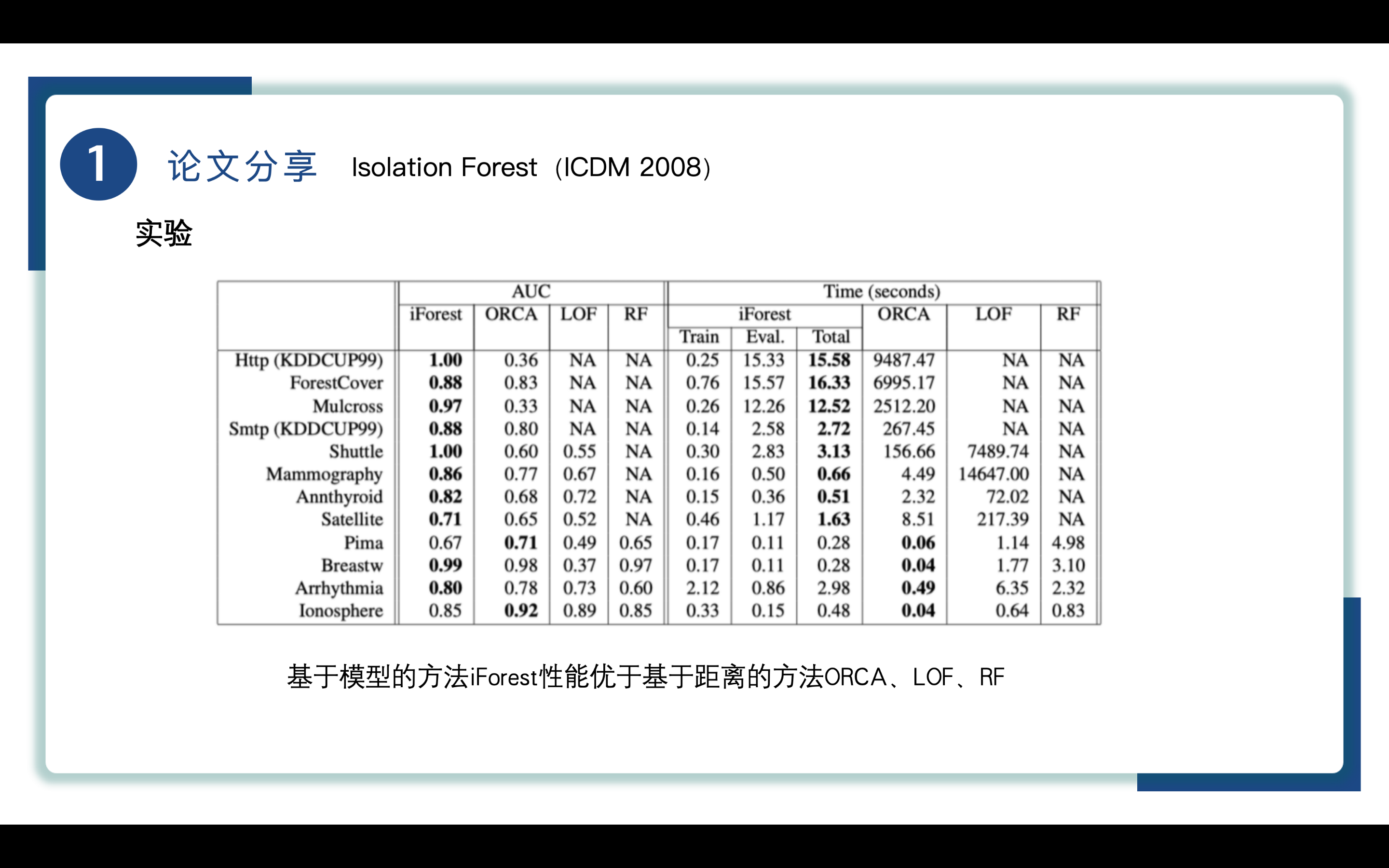
通过比较AUC可知基于模型的方法iForest性能优于基于距离的方法ORCA、LOF、RF。

因为iForest不需要取计算数据之间的距离，这为iForest提供了巨大优势。

ORCA和其他类似的基于k近邻的方法存在一个问题：它们只能检测到大小小于k的低密度异常簇。增加k可以解决这个问题，但在高容量数据集会增加处理时间。

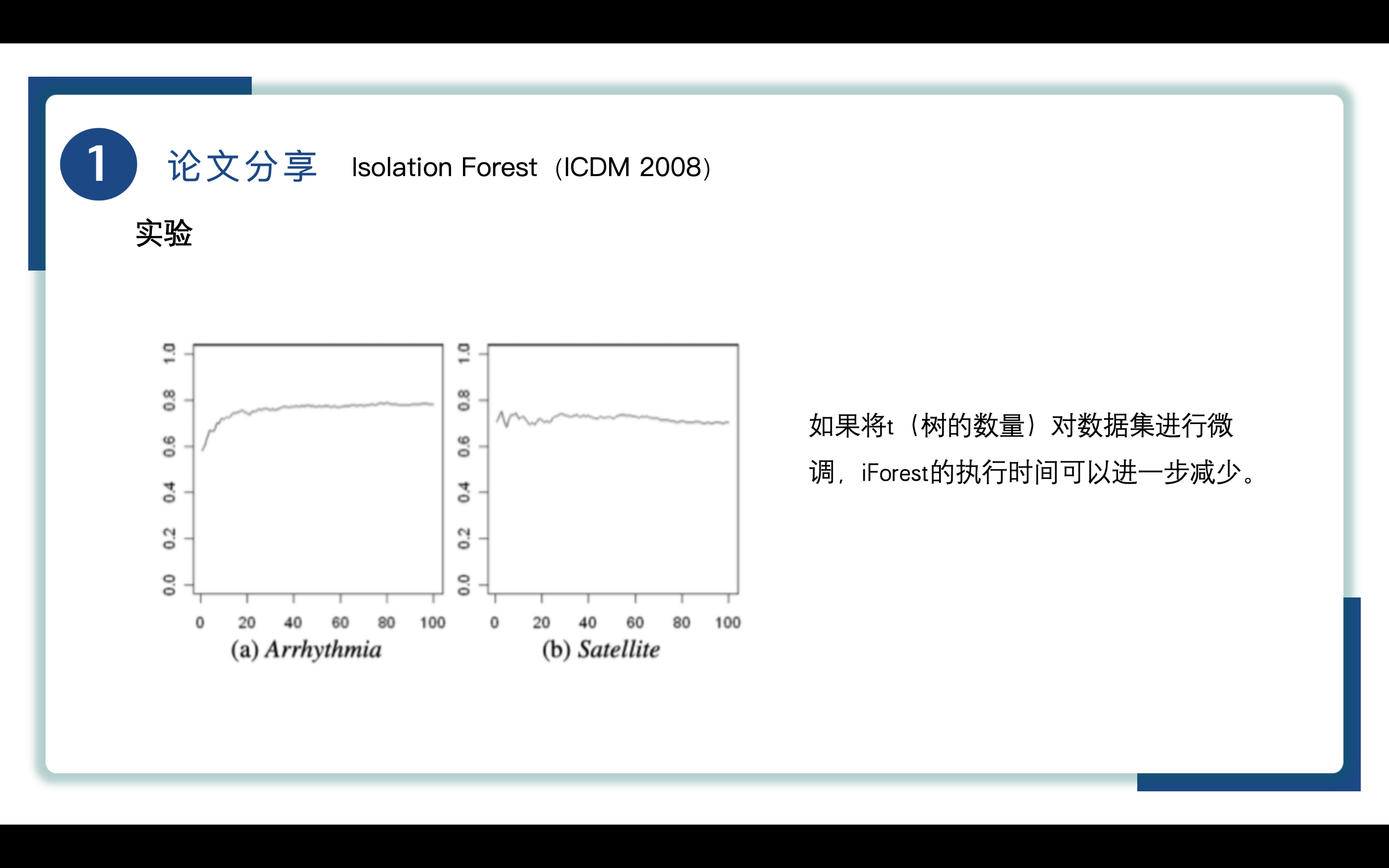
如图所示，x轴为t，y轴为AUC，如果将t（树的数量）对数据集进行微调，选择合适的t，避免不必要的计算，使iForest的执行时间可以进一步减少。

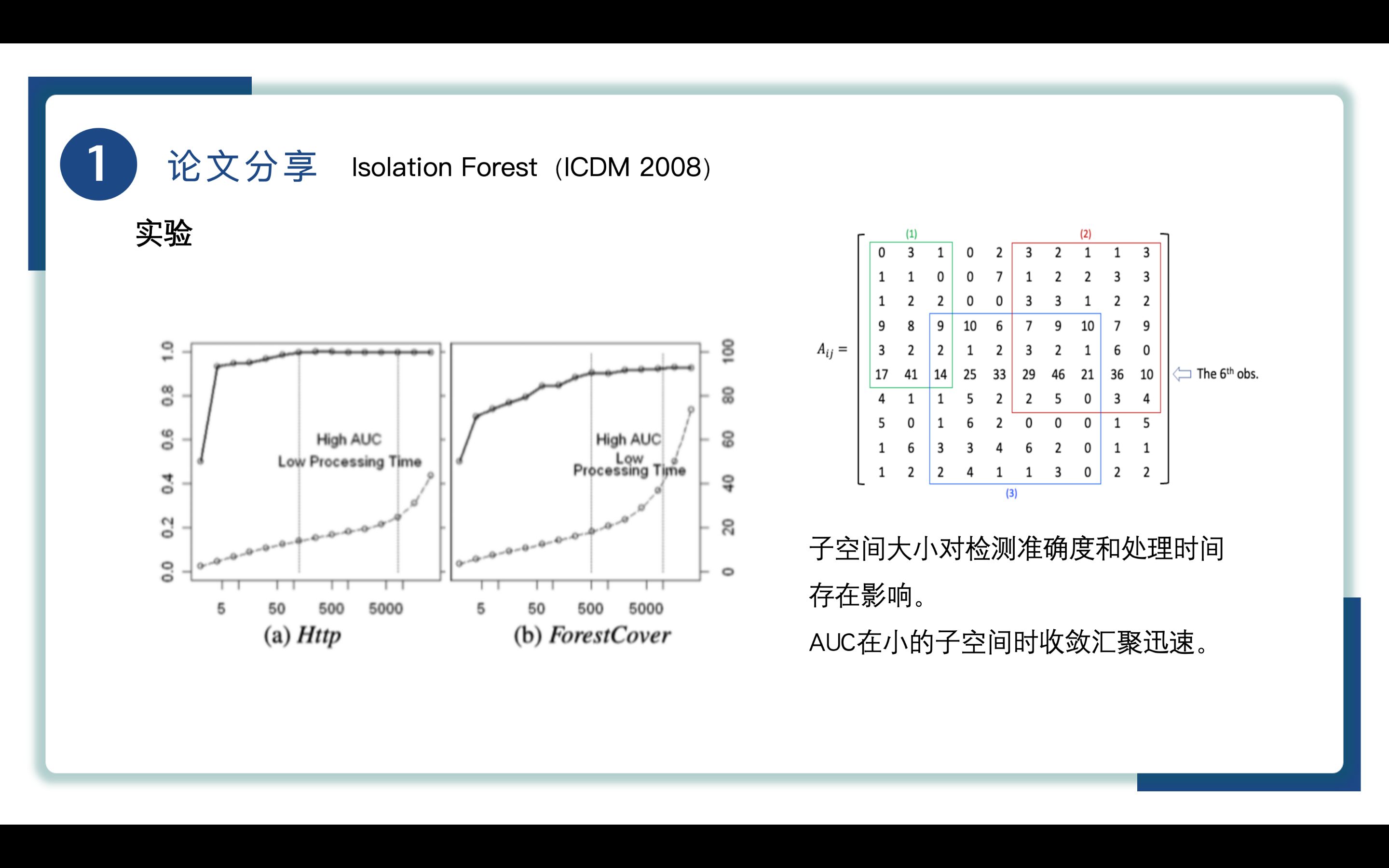
右图给出了子空间的示例，在这里一行为一个实例，一列为实例的一个特征，第i个样本有j个特征，通过随机划定样本和特征大小创造子空间进行划分计算。

如左图所示，x轴为子空间的大小，y轴实线为AUC，虚线为处理时间，可以知道AUC在小的子样本时收敛汇聚迅速，子样本大小对检测准确度和处理时间的存在影响。

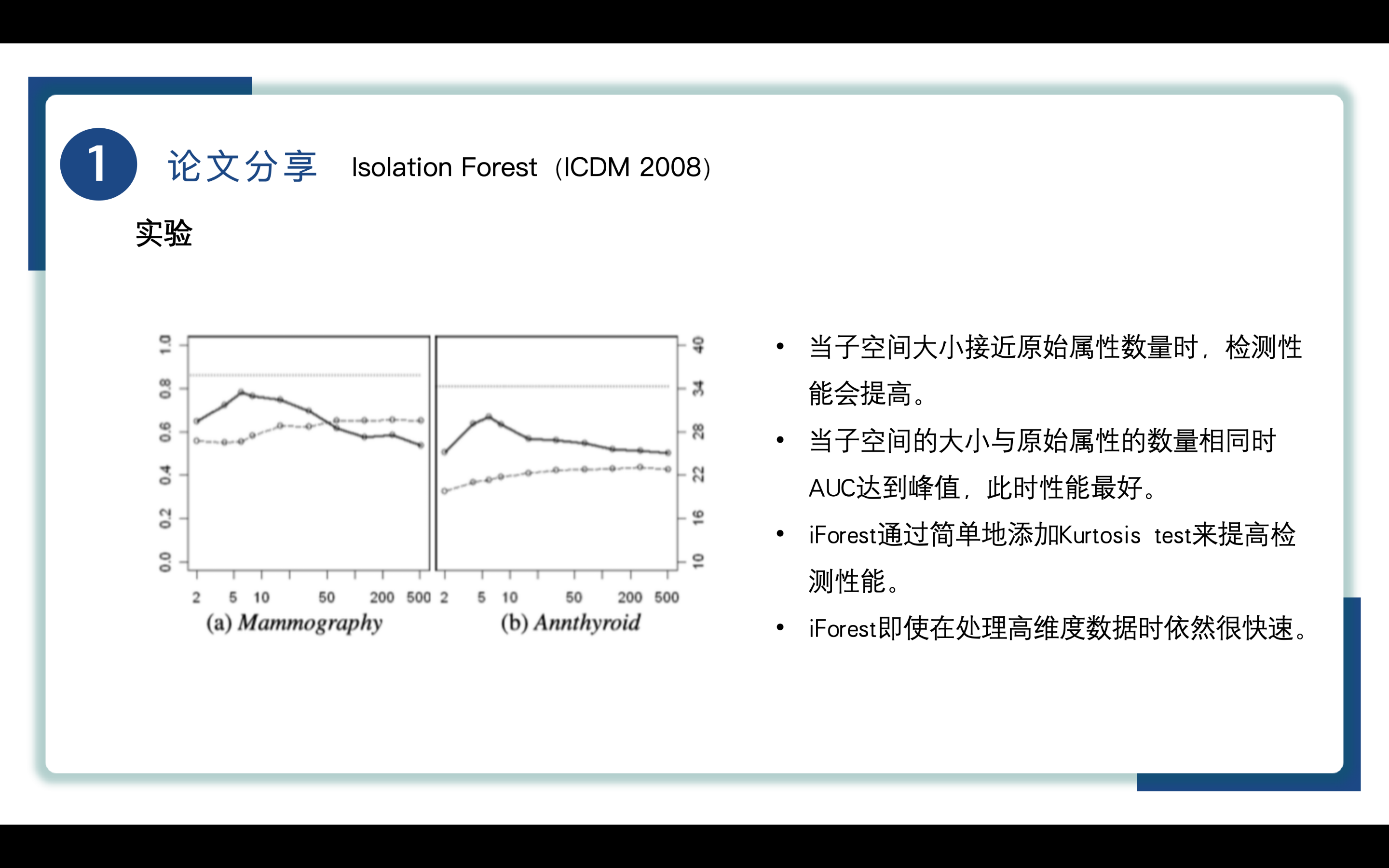
随后作者通过使用不同的取子空间大小对iForest的性能进行了分析，如图所示，图中y轴实线为AUC、y轴虚线为处理时间，x轴为子空间大小，实验结果表明当子空间大小接近原始属性数量时，检测性能会提高。当子空间的大小与原始属性的数量相同时AUC达到峰值，此时性能最好。iForest通过简单地添加Kurtosis test（峰度检验）来评估数据分布的尖峭程度，尤其是在数据分布不均或存在明显异常值的情况下。可以增强模型对异常值的敏感性，能够帮助识别数据中的异常值以提高检测性能，

得益于随机抽样、特征选择、有效的树构建策略以及算法优化的策略，iForest即使在处理高维度数据时依然很快速。

总结

最后对iForest做个总结，iForest算法拥有较低的计算复杂度，能够快速执行、拥有低内存需求，收敛速度快，只需小的样本量就能检测，侧重于异常隔离，在高维度和无异常实例数据上也表现良好，对处理大容量数据库拥有实际应用意义。

参考资料

• https://blog.csdn.net/wjjc1017/article/details/135842183

• https://blog.csdn.net/qq_34160248/article/details/124538485

• https://blog.csdn.net/ewen_lee/article/details/109892412